Commenter (distribution)

[aviateur]

Si, la position d'une particule X suit une loi normale quelque soit t.
A
et cela se calcule très bien et ça ne dépend pas de x_0 (ou de t_0). Après il y a des tables ou une calculatrice pour avoir une valeur approchée. Mais au départ c'est un calcul intégral à faire.

[Ben314]

Salut,
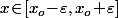
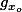
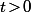
Perso, ce que j'aurais écrit, c'est que la proba. qu'à l'instant , la particule soit "à peu prés" en , c'est à dire que la variable aléatoire (pour un petit fixé) c'est exactement égal à donc c'est approximativement égal à . Donc le maximum de la fonction représente l'instant où la proba que la particule soit à peu prés en est la plus forte.
Et on peut noter qu'il est "assez remarquable" que cette valeur soit la même que celle de la distance moyenne que l'on obtient à l'instant : un des deux représente une moyenne alors que l'autre, c'est plus ou moins un "mode" (c'est à dire "la classe ayant le plus grand effectif" en statistique descriptive). En général, ce sont des valeurs différentes.

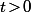
P.S. : Le "à peu prés" me semble important vu que par définition même d'une loi à densité, la proba. que la particule soit exactement (au sens mathématique) à un endroit donné à l'instant est systématiquement nulle.

[aviateur]

@ ben, le remarquable a été dit je crois ? D'autre part, je ne pense pas avoir parlé de la probabilité pour une particule d'être en x_0 mais plutôt de sa densité de proba en x_0. Bref c'est pas inutile de mette les points sur les i.
Par contre, je ne sais pas si tu as vu mais @qaterio a évoqué l'entropie d'un tel système. Est-ce que tu aurais une définition précise de l'entropie d'un tel système (si entropie il y a). ?

[LB2]

Il y a plusieurs notions d'entropies qui coincident mais c'est tout un cours de physique statistique si on veut le détailler...

Entropie de Boltzmann d'un système S=k*ln(Nb d'états possibles du système) et k la constante de Boltzmann

[Ben314]

@aviateur : la notion "d'entropie", à part vaguement à quoi ça correspond en terme intuitif, j'y connaît que dalle.
Sinon, dans mon post, je ne donne que et exclusivement que "ce que j'aurais écrit" si c'était moi le candidat et il ne faut y voir aucune critique ni même un quelconque commentaire concernant les post précédents vu que je les ai à peine survolés.

[aviateur]

rebjr
^beb J'y ai pas vu de critique dc no pb.
Pour l'entropie "niveau du désordre" ça serait bien <x^2>=2Dt qui donne la dispersion moyenne en fonction du temps. Mais bref, c'est pas sûr" et je conseille à @qaterio de ne pas en parler au risque de faire comme si on savait sans savoir.