Comment diviser une somme arithmétique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par mightysoldier001 » 31 Mai 2017, 18:36
par mightysoldier001 » 31 Mai 2017, 18:36
Bonjour,
Je suis tombé sur ça
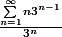
Comment je le simplifie? Puis-je simplement intégrer la fraction dans la somme?
Merci

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Mai 2017, 19:08
par zygomatique » 31 Mai 2017, 19:08
salut
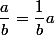
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 31 Mai 2017, 19:31
par pascal16 » 31 Mai 2017, 19:31
l'écriture n'est pas bonne
le n à l'intérieur de la somme varie à chaque fois
le n en dessous lui ne varie pas.
il y a interférence entre les deux "n".
si la somme s’arrêterait à N, et en bas que se soit N aussi, et qu'on cherche la limite quand N tend vers l'infini, on aurait une définition correcte.
sinon, on applique les règles de distributivité classiques
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 01 Juin 2017, 14:12
par Pythales » 01 Juin 2017, 14:12
C'est plutôt la limite de l'expression
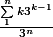
lorsque n tend vers l'infini
(c'est équivalent à n/3)
Modifié en dernier par
Pythales le 03 Juin 2017, 10:31, modifié 1 fois.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 03 Juin 2017, 00:46
par aymanemaysae » 03 Juin 2017, 00:46
Bonsoir ;
Je suivrai le chemin tracé par Pythales :
Soit
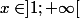
: cette ligne a été modifiée suite à la remarque de Pascal .
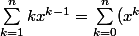' = (\Sum_{k = 0} x^k)'=(\frac{x^{n + 1} - 1}{x - 1})')
x^n(x - 1) - x^{n + 1} + 1}{(x - 1)^2} = \frac{(n + 1)x^{n + 1} - (n + 1)x^n - x^{n + 1} + 1 }{x^2 - 2 * x + 1}= \frac{nx^{n + 1} - (n + 1)x^n + 1}{x^2 - 2 * x + 1} ,)
donc :
x^n + 1}{x^{n + 2} - 2 * x^{n + 1} + x^n})
donc :
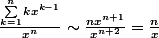
quand n tend vers
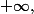
donc si x = 3 , on a :
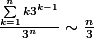
quand n tend vers

On remarque une petite différence avec le résultat obtenu par Pythales :

quand n tend vers

.
Modifié en dernier par
aymanemaysae le 03 Juin 2017, 14:39, modifié 1 fois.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 03 Juin 2017, 08:11
par pascal16 » 03 Juin 2017, 08:11
il me semble qu'il faudrait refaire le calcul pour x négatif car les équivalences ne marchent plus.
dans ]0;1[, le terme prédominant doit y être inversé.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 03 Juin 2017, 14:37
par aymanemaysae » 03 Juin 2017, 14:37
Bonjour ;
pascal16 a écrit:il me semble qu'il faudrait refaire le calcul pour x négatif car les équivalences ne marchent plus.
dans ]0;1[, le terme prédominant doit y être inversé.
La remarque de Pascal est fondée , et pour cause, j'ai rectifié ma réponse sus mentionnée .
Merci pour l'attention que tu as portée à ma réponse .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités