Cns

[jeje56]

Bonjour,

Voici l'exercice :

On cherche une CS pour qu'il existe X tq X²=A, X et A matrice carrées réelles, A diagonalisable : les VP de A positives ou nulles est une solution

Est-ce une CN ?
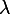
Pour cela on pose en dimension 2 : et on trouve que pour négatif strictement, il existe X tq X²=A

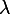
Je ne comprends pas le avec VP de A... Pourquoi peut-on poser ceci ?

Merci bcp !

[XENSECP]

Etrange je te l'accorde :)

[yos]

on pose en dimension 2 :

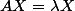
C'est pas plutôt on "résout" d'inconnue X dans ?

[jeje56]

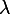
Non justement, on résout en fait : ... en posant a,b,c,d comme coefficients de X (ce sont les inconnues), étant fixé négatif strictement... et on trouve que le système obtenu a une solution...

Bizarre...

[yos]

Ca veut dire que ta CS est pas N.

[jeje56]

On est d'accord pour le résultat... Mais c'est la forme qui me pose problème... la rédaction !

:-)

[jeje56]

est peut-être un cas particulier... ?

Quelqu'un a-t-il une idée ?

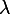
Edit : comme VP associé à , , on cherche X tq ?

[yos]

Qu'est-ce qui ne va pas? Tu as une matrice diagonalisable (car diagonale) à valeurs propres < 0 admettant une racine carrée. Cela prouve bien que la positivité des valeurs propres n'est pas une CN d'existence de racine carrée.

[jeje56]

Tu as une matrice diagonalisable (car diagonale) à valeurs propres < 0

C'est juste ça qui me gène... Pourquoi par exemple les deux VP sont égales ? De quelle polynôme sont-elles les solutions ?

[Roman]

Bonjour,

En fait, on pourrait poser n'importe qu'elle matrice "qui nous arrange".

Le but c'est de trouver une matrice A qui vérifie la négation de "les VP de A positives ou nulles" et qui soit solution.

La forme la plus simple possible c'est lamba*I2 (a priori)...

Si ça n'avait pas marche avec cette matrice la, peut être qu'on aurait du prendre 2 valeurs propres distinctes... Ou peut être même qu'on aurait pris une matrice 2x2 quelconque pour voir ce que ça donnait...

Roman

[jeje56]

D'accord, je vois... Merci Roman