CNS d'existence d'une racine multiple

[kingsize]

Bonjour,

Voici un exo sur les polynômes sur lequel je sèche :

Soit P = X^3 + pX + q un polynôme de degré 3 avec p et q des nombres complexes. Trouver une CNS sur p et q pour que P admette une solution multiple (dans l'ensemble des complexes).

Bon, c'est un thème classique et il est connu qu'une CNS est 27q² + 4p^3 = 0.

Voici ce que j'ai fait : P admet une racine multiple si et seulement si il existe un complexe x tel que P(x) = P'(x) = 0. Après quelques calculs faciles, cela équivaut à l'existence d'un complexe x tel que x² = -p/3 et x^3 = q/2.
A partir de là, si P admet une racine multiple, il suffit alors d'élever au cube la première égalité et au carré la seconde, puis de les égaliser et on trouve bien 27q² + 4p^3 = 0.

Par contre, pour montrer que cette condition est suffisante, je coince. Il suffit de montrer l'existence d'un complexe x tel que x² = -p/3 et x^3 = q/2. Or, on sait que l'équation x² = -p/3 admet au moins une solution complexe (une seule si p =0, exactement deux si p est non nul). Mais parmi ces solutions, comment montrer qu'au moins une d'elles vérifient x^3 = q/2 ? Si quelqu'un avait une piste, je lui en saurais gré.

Merci.

[chan79]

salut
si =0, alors p est négatif

il existe alors un réel a tel que

donc

avec

on vérifie facilement que

[deltab]

Bonjour

Mais ici et sont des nombres complexes.
La solution qu'avait proposé Chan79 (post suivant s'il ne l'a pas enlevé) correspond au cas et réels.

On peut utiliser un résultat plus général:
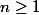Un polynôme de degré admet pour racine multiple d'ordre si et seulement si et toutes ses dérivées s'annulent en .

Si le résultat est connu, tant mieux (il n'est pas de démonstration difficile) sinon dans notre cas, on l'énonce et le démontre pour au moins une racine double ce qui revient à montrer pour la réciproque que si et alors admet au moins comme racine double.

En effet supposons que , alors

d'où.

Comme alors et on peut écrire et on aura ce qui prouve que est au moins une racine double de .

En appliquant ce résultat, on aura:

[chan79]

Mais ici et sont des nombres complexes.
La solution que tu as proposée correspond au cas et réels.
On peut utiliser un résultat plus général: Un polynôme de degré admet x_0 pour racine multiple d'ordre si et seulement si et toutes ses dérivées s'annulent en x_0.
Si le résultat est connu, tant mieux (il n'est pas de démonstration difficile) sinon dans notre cas, on l'énonce et le démontre pour au moins une racine double ce qui revient à montrer pour la réciproque que si et alors P(x) admet au moins comme racine double.

Exact
J'enlève mon message
Merci