Classe à gauche
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 18 Jan 2024, 20:29
par chombier » 18 Jan 2024, 20:29
Bonjour,
J'ai une question dont je cherche désespérément une réponse.
Soit G un groupe,
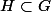
un sous-groupe de G et
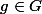
un élément de G.
J'ai la conviction très forte que si
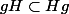
alors
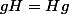
. Je n'arrive pas à imaginer que cela pourrait être faux.
Si H est fini, la réponse est trivialement oui car ces deux ensembles ont le même cardinal.
Si H est infini... je sèche. Je sèche tellement que je finis pas penser que c'est faux, mais je ne trouve pas non plus de contre-exemple.
Des idées ? Merci d'avance !!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Jan 2024, 23:41
par Ben314 » 18 Jan 2024, 23:41
Salut,
J'ai l'impression d'avoir un contre exemple :
Pour tout
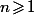
, soit

le groupe des bijection de
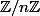
sur lui même et

le produit des

.
On considère l'ensemble

des
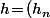_{n\geq 1}\!\in\!G)
tels qu'il existe un entier

tel que
\!=\!x)
.
Sauf erreur, c'est bien un sous groupe de

.
On considère alors l'élément
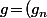_{n\geq 1}\!\in\!G)
défini par :
\!=\!x\!+\!1)
.
Et il me semble bien qu'on a alors
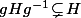
.
C'est à vérifier proprement vu que j'ai rien regardé dans le détail et, si c'est correct (???), il y a sans doute bien plus simple sur le même principe.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
