Ideaux à gauche de Mn(K)

[Charmander]

Bonjour,

Soit I un déal à gauche de Mn(K). Montrer qu'il existe une matrice telle que I={AP|AMn(K)} et . On note r le rang maximal des matrices dans I.

Dans l'exercice précédent, on avait démontré avec des observations astucieuses que si J_r était dans I, alors P=Jr convient. Mais maintenant on ne sait plus si Jr est dans I, et il n'y a pas de raison qu'il y soit. Donc comment faire ? La condition que P soit un projecteur me gêne beaucoup.
Merci d'avance.

[zygomatique]

salut

pour deux matrices A et P compare les noyaux de P et AP ....

[Charmander]

Bonjour,

KerP est inclus dans KerAP ? Je vois pas comment l'exploiter

[zygomatique]

donc

il suffit alors de considérer la matrice de I de plus petit rang ....

[Charmander]

Ah oui , comme pour tout A, dim(KerP)<dim(KerAP), pour P de rang minimal on doit avoir rg(AP)=rg(P) pour tout A avec le theoreme du rang. Donc

Mais ça ne veut toujours pas dire que I=AP :/

[zygomatique]

c'est un peu plus compliqué que cela ....

puisque P est un projecteur considère une base constituée d'une base de son noyau et d'une base de son image .....

[Charmander]

Bonjour,

Dsl pour le retard de ma réponse. J'ai compris comment faire une fois qu'on a montré que P est un projecteur. Il reste qu'un détail qui me gêne : êtes vous sûr que P est un projecteur ? Car c'est bien de montrer que rg(P2)=rg(P) puis KerP+ImP = K^n en somme directe, mais cela ne suffit pas pour dire que P est un projecteur, non ?

[Ben314]

... êtes vous sûr que P est un projecteur ?

Vu que tu dit pas un traitre mot de comment tu as "choisi" ce fameux P, je vois pas trop comment on pourrait être sûr (ou pas) que ton P est un projecteur...

De toute façon, le coté "P projecteur", c'est vraiment pas ça la difficulté dans l'exo : si tu prend l'idéal à gauche engendré par une certaine matrice B (quelconque), c'est a dire l'ensemble des AB avec A dans Mn(K), il te suffit d'écrire que B=U.Jr.V avec U,V inversible pour voir que l'idéal en question est aussi engendré par P=V^-1.U^-1.B=V^-1.Jr.V qui est un projecteur.

[Charmander]

Merci, votre remarque résout parfaitement mon problème.
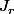
Une fois qu'on a montré que est dans I, il suffit de remarquer que est alors un idéal à gauche qui contient PV donc donc , et comme la composition par un isomorphisme conserve le rang, r est toujours le rang maximal des matrices de .
On peut alors appliquer le résultat de l'exercice précédent, = { | A M_n(K)}.
Or est un isomorphisme, donc { |A } = { | A M_n(K)}
D'ou = { | A M_n(K)}
Puis I={| A M_n(K)} = {AP | A M_n(K)} avec
Etes-vous d'accord ?

[Ben314]

Oui, ça me semble parfaitement correct.

[Charmander]

Très bien, merci beaucoup ! :)

[roket]

Bonjour,

Dsl pour le retard de ma réponse. J'ai compris comment faire une fois qu'on a montré que P est un projecteur. Il reste qu'un détail qui me gêne : êtes vous sûr que P est un projecteur ? Car c'est bien de montrer que rg(P2)=rg(P) puis KerP+ImP = K^n en somme directe, mais cela ne suffit pas pour dire que P est un projecteur, non ?

Bah si, c'est justement la définition, toute application linéaire u telle que Ker u + Im u = K^n en somme directe est la projection sur Im u parallèlement à Ker u.

[roket]

Merci, votre remarque résout parfaitement mon problème.
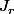
Une fois qu'on a montré que est dans I, il suffit de remarquer que est alors un idéal à gauche qui contient PV donc donc , et comme la composition par un isomorphisme conserve le rang, r est toujours le rang maximal des matrices de .
On peut alors appliquer le résultat de l'exercice précédent, = { | A M_n(K)}.
Or est un isomorphisme, donc { |A } = { | A M_n(K)}
D'ou = { | A M_n(K)}
Puis I={| A M_n(K)} = {AP | A M_n(K)} avec
Etes-vous d'accord ?

Pour montrer l'existence on peut aussi utiliser un lemme de factorisation : (exo feuille chapitre 10)
Soit M une matrice qcq, il existe G dans Gln et P un projecteur tel que :

M = GoP

On applique ça à une matrice M dans I de rang r :

M = GoP, donc G^-1 M = P est dans I.