Bonjour à tous,
J'aimerais avoir des explications concernant une problématique qui me semble plutôt simple mais je ne me souviens plus le pourquoi du comment....
ci dessous le lien d'une image pour illustrer mes propos :
https://fr.wikipedia.org/wiki/Rotation_ ... onaxes.png
Je souhaite faire le liens entre les différents axes après un changement de plan ( soit un plan xOy et x'Oy' d'angle a).
soit x' = x cos(a) - y sin(a)
y' = -x sin(a) + y cos(a)
et en retournant l'équation :
x = x' cos(a) - y' cos(a)
y= x' sin(a) + y' sin(a)
Pourriez vous m'expliquer le résonnement à suivre pour avoir le résultat ci dessous et surtout le choix des signes ?
En vous remerciant par avance pour votre temps et vos informations.
Changement de référentiel trigonometrique
3 messages
- Page 1 sur 1
Re: Changement de référentiel trigonometrique
Salut,
Pssst : résonner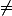 raisonner (c'est LA faute qui fait passer pour une vrai cloche...)
raisonner (c'est LA faute qui fait passer pour une vrai cloche...)
Sinon, au départ, tu as un repère (orthonormé direct)) du plan.
du plan.
Ensuite, tu as un deuxième repère (orthonormé direct)) .
.
Comme est de norme 1, il a des coordonnées (dans
est de norme 1, il a des coordonnées (dans  ) de la forme
) de la forme ,\sin(\theta))) (où
(où  est l'angle orienté de
est l'angle orienté de 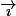 vers
vers  ) et, comme
) et, comme  est obtenu en partant de
est obtenu en partant de  par rotation de 90° dans le sens direct, c'est qu'il a comme coordonnées (dans
par rotation de 90° dans le sens direct, c'est qu'il a comme coordonnées (dans  )
) ,\cos(\theta))) (fait un dessin pour te convaincre que si on tourne de 90° dans le sens direct un vecteur de coordonnées (X,Y) on obtient le vecteur de coordonnées (-Y,X)).
(fait un dessin pour te convaincre que si on tourne de 90° dans le sens direct un vecteur de coordonnées (X,Y) on obtient le vecteur de coordonnées (-Y,X)).
Bilan :\vec{\imath}\!+\!\sin(\theta)\vec{\jmath}\cr\vec{\jmath}'=-\sin(\theta)\vec{\imath}\!+\!\cos(\theta)\vec{\jmath}\end{matrix}\right.)
Maintenant, si un point a pour coordonnées
a pour coordonnées ) dans
dans  , ca signifie que
, ca signifie que  et on en déduit que :
et on en déduit que :
\vec{\imath}\!+\!\sin(\theta)\vec{\jmath}\Big)+y'\Big(-\sin(\theta)\vec{\imath}\!+\!\cos(\theta)\vec{\jmath} \Big))
x'\!-\!\sin(\theta)y'\Big)\vec{\imath}+\Big(\sin(\theta)x'\!+\!\cos(\theta)y'\Big)\vec{\jmath})
Donc ce même point a pour coordonnées
a pour coordonnées x'\!-\!\sin(\theta)y'\,;\,\sin(\theta)x'\!+\!\cos(\theta)y'\Big)) dans le repère
dans le repère  .
.
Pour obtenir le changement de variable "dans l'autre sens", il y a plusieurs méthodes :
- Soit on "inverse" les relations donnant en fonction de
en fonction de  et on réécrit les deux lignes de calcul ci dessus en partant de
et on réécrit les deux lignes de calcul ci dessus en partant de  .
.
- Soit on inverse directement les formules obtenues ci dessus donnant en fonction de
en fonction de 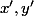 .
.
- Soit on a un peu de bon sens et on se dit que, si pour passer de à
à  on a tourné de
on a tourné de  , alors pour passer de
, alors pour passer de  à
à  il faut tourner de
il faut tourner de 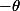 donc les autres formules, c'est les même que les premières où on a remplacé
donc les autres formules, c'est les même que les premières où on a remplacé  par
par 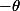 .
.
Pssst : résonner
Sinon, au départ, tu as un repère (orthonormé direct)
Ensuite, tu as un deuxième repère (orthonormé direct)
Comme
Bilan :
Maintenant, si un point
Donc ce même point
Pour obtenir le changement de variable "dans l'autre sens", il y a plusieurs méthodes :
- Soit on "inverse" les relations donnant
- Soit on inverse directement les formules obtenues ci dessus donnant
- Soit on a un peu de bon sens et on se dit que, si pour passer de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Changement de référentiel trigonometrique
Bonjour !
... une vraie cloche ce serait bien aussi !
Pour l'inverse on peut aussi noter que la matrice de passage est orthogonale donc l'inverse n'est autre que la transposée.
... une vraie cloche ce serait bien aussi !
Pour l'inverse on peut aussi noter que la matrice de passage est orthogonale donc l'inverse n'est autre que la transposée.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
