Il est clair que si
Champ vectoriel
7 messages
- Page 1 sur 1
Champ vectoriel
Bonjour à tous, je m'intéresse aux conditions pour qu'un champ vectoriel 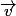 soit le gradient d'un champ scalaire
soit le gradient d'un champ scalaire  . Autrement dit étant donné
. Autrement dit étant donné 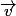 je me demande quelles sont les conditions pour l'existence de
je me demande quelles sont les conditions pour l'existence de  telle que :
telle que :
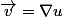
Il est clair que si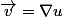 alors
alors 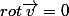 mais pour la réciproque je pense qu'il y a des conditions supplémentaires... Si quelqu'un peut m'éclairer merci.
mais pour la réciproque je pense qu'il y a des conditions supplémentaires... Si quelqu'un peut m'éclairer merci.
Il est clair que si
Pas besoin d'être étoilé (ca c'est pour la dérivation d'un potentiel vectoriel), mais juste simplement connexe.
Tu peux généraliser à R^N avec ceci:
Soit un ouvert simplement connexe. Ton champ dérive d'un potentiel scalaire sur cet ouvert ssi sa matrice jacobienne est symétrique sur cet ouvert.
Tu vérifie facilement qu'en posant R=3, t'obtiens rot=0.
Tu peux généraliser à R^N avec ceci:
Soit un ouvert simplement connexe. Ton champ dérive d'un potentiel scalaire sur cet ouvert ssi sa matrice jacobienne est symétrique sur cet ouvert.
Tu vérifie facilement qu'en posant R=3, t'obtiens rot=0.
Comme l a dit Arkhnor, ça ne pose aucun problème.
Effectivement la jacobienne est symétrique sur R^2\{(0,0)}, mais ce n'est pas simplement connexe... Donc on ne peut rien conclure a priori.
En intégrant sur le cercle de centre (0,0) et de rayon 1, on voit directement que l'intégrale est non nulle et donc il ne peut pas exister de potentiel scalaire pour ce champ.
(Par contre en si tu étend ce champ à R^3 et en posant la troisième coordonnée nulle, il existe un potentiel vectoriel.)
Effectivement la jacobienne est symétrique sur R^2\{(0,0)}, mais ce n'est pas simplement connexe... Donc on ne peut rien conclure a priori.
En intégrant sur le cercle de centre (0,0) et de rayon 1, on voit directement que l'intégrale est non nulle et donc il ne peut pas exister de potentiel scalaire pour ce champ.
(Par contre en si tu étend ce champ à R^3 et en posant la troisième coordonnée nulle, il existe un potentiel vectoriel.)
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
