C'est pourtant exactement ça. Bon, puisque tu refuses obstinément de comprendre mes indications, je ne vois pas d'autre moyen que de faire moi-même la démonstration.
On a une chaîne de Markov avec un ensemble d'état
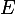
fini, dont la matrice de transition est
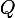
.
Pour tout entier naturel
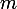
,

est la variable aléatoire dont la valeur est l'état après
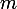
étapes. On a, pour tout
\in E^2)
,
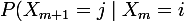= Q(i,j))
.
On veut montrer que pour tout entier naturel

,
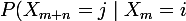= Q^n(i,j)\qquad(\ast))
.
On fait une démonstration par récurrence sur

.
Initialisation : pour

, c'est la définition de matrice de transition.
Hérédité : on suppose
)
pour un entier

et on veut le montrer pour

.
Les événements

pour

forment un système complet d'événements. Donc
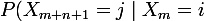= \sum_{k\in E} \left(P(X_{m+n}=k\mid X_m=i)\times P(X_{m+n+1}=j\mid P(X_{m+n}=k)\right))
.
D'accord ? (C'est ce que j'essayais de te faire comprendre, sans succès, avec "aller de
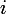
à
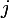
en

étapes est une disjonction de cas qui s'excluent l'un l'autre : pour chaque état

, aller de
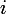
à

en

étapes puis aller de

à
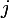
en une étape".)
En utilisant l'hypothèse de récurrence, on en déduit
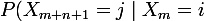= \sum_{k\in E} \left(Q^n(i,k)\times Q(k,j)\right)=Q^{n+1}(i,j))
,
la dernière égalité venant de la définition du produit de matrices. Ceci termine la démonstration de
)
par récurrence.
