Cardinal
12 messages
- Page 1 sur 1
Cardinal
BOnjour, j'aimerais dénombrer l'ensemble suivant, i.e calculer card A avec
n dans N et
A={k dans {0,....,n} tel que (k parmi n) est impair}
après calcul, je me suis aperçu que c'était une puissance de 2, il y a surement une histoire de modulo mais je ne vois pas comment trouver une formule adéquate. Si quelqu'un a une démonstration a cela, ce serait fort aimable, merci d'avance
n dans N et
A={k dans {0,....,n} tel que (k parmi n) est impair}
après calcul, je me suis aperçu que c'était une puissance de 2, il y a surement une histoire de modulo mais je ne vois pas comment trouver une formule adéquate. Si quelqu'un a une démonstration a cela, ce serait fort aimable, merci d'avance
un truk bizarroïde
re,
j'ai vû un truc bizzaroïde en essayant de résoudre cet exercice:
pour expliquer simplement, je remonterai dans l'alphabet:
v,u,t,s,r,q,p..
on sait que si (v_n) est le terme général d'une suite, on peut considérer
sa suite dérivée
formée des différences divisées et réitérer le procédé:

quand on itère les différences divisées:
 (**)
(**)
on voit qu'on obtient une égalité (**)
, qui, formellement, a comme coefficients de la combinaison linéaire, ceux du développement de^3)
Maintenant, on applique cette remarque au triangle de Pascal,
que l'on complète par des zéros à droite et au dessus.
la suite) (c'est l'indice n de ligne qui varie)
(c'est l'indice n de ligne qui varie)
des coeff d'une colonne du tableau a pour différence divisée
la suite formée des coeff. de la colonne précédente.
d'indice k-1
à cause de
 - ( _k^{n} ) = ( _{k-1}^{n} ))
en itérant les différences divisées de la suite,
formée des coeff. d'une colonne,
on se ramène, en un nombre fini d'étapes, au bord gauche du tableau,
sur la colonne des 1.
on en déduit que n'importe quelle suite, formée des coefficients
d'une colonne k (k fixé) du triangle, vérifie une récurrence linéaire
d'ordre k, d'équation caractéristique^k=0)
et va s'exprimer comme combinaison linéaire de .... je me souviens plus quoi au juste :hum:
je me demande si on peut exprimer les coefficients du binôme
avec des combinaisons linéaires de polynômes de Bernoulli :biere:
Comme la différence divisée est un opérateur linéaire, sur l'espace des suites, qui ressemble fort à une dérivation:
 \rightarrow (v)=(v_n=\frac{u_{n+1}-u_{n}}{(n+1)-n})=u')
on "primitive" inversement la suite (u_n) en

mézalor,on doit avoir une formule d'intégration du style
 = \int_{0}^n \, (_{k-1}^t) d\mu(t)) où l'on a remplacé le sigma par une intégrale,
où l'on a remplacé le sigma par une intégrale,
avec la mesure de comptage.
j'ai vû un truc bizzaroïde en essayant de résoudre cet exercice:
pour expliquer simplement, je remonterai dans l'alphabet:
v,u,t,s,r,q,p..
on sait que si (v_n) est le terme général d'une suite, on peut considérer
sa suite dérivée
formée des différences divisées et réitérer le procédé:
quand on itère les différences divisées:
on voit qu'on obtient une égalité (**)
, qui, formellement, a comme coefficients de la combinaison linéaire, ceux du développement de
Maintenant, on applique cette remarque au triangle de Pascal,
que l'on complète par des zéros à droite et au dessus.
la suite
des coeff d'une colonne du tableau a pour différence divisée
la suite formée des coeff. de la colonne précédente.
d'indice k-1
à cause de
en itérant les différences divisées de la suite,
formée des coeff. d'une colonne,
on se ramène, en un nombre fini d'étapes, au bord gauche du tableau,
sur la colonne des 1.
on en déduit que n'importe quelle suite, formée des coefficients
d'une colonne k (k fixé) du triangle, vérifie une récurrence linéaire
d'ordre k, d'équation caractéristique
et va s'exprimer comme combinaison linéaire de .... je me souviens plus quoi au juste :hum:
je me demande si on peut exprimer les coefficients du binôme
avec des combinaisons linéaires de polynômes de Bernoulli :biere:
Comme la différence divisée est un opérateur linéaire, sur l'espace des suites, qui ressemble fort à une dérivation:
on "primitive" inversement la suite (u_n) en
mézalor,on doit avoir une formule d'intégration du style
avec la mesure de comptage.
bon , attends, on va essayer de réfléchir à TON énoncé.
Je m'étais un peu égaré sur le sujet "les coefficients binomiaux
forment une séquence de primitives, à relier aux polynômes de Bernoulli
et au calcul formel". revenons à nos moutons.
As tu écrit un triangle de Pascal de taille raisonnable (20x20) pour conjecturer ?
on doit pouvoir l'écrire en modulo 2
Je m'étais un peu égaré sur le sujet "les coefficients binomiaux
forment une séquence de primitives, à relier aux polynômes de Bernoulli
et au calcul formel". revenons à nos moutons.
As tu écrit un triangle de Pascal de taille raisonnable (20x20) pour conjecturer ?
on doit pouvoir l'écrire en modulo 2
re,
ce n'est pas pour être méchant (en fait , si), mais si on écrit
un triangle de Pascal modulo 2, avec des 1 et 0, en remplaçant
+(_{k+1}^n)=(_{k+1}^{n+1}))
par leur parité 0-1, on "voit" de jolies choses:
les lignes de rang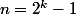 ne comportent que des 1
ne comportent que des 1
les coeff en colonne forment une suite périodique (j'en suis pas si sûr)
j'imagine des relations polynomiales entre les périodes
de suites formées des coefficients d'une colonne.
les lignes d'indice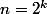 comportent juste deux "1" aux extrémités.
comportent juste deux "1" aux extrémités.
ça doit être lié à l'exponentiation
^2=2^{2^{k+1}})
est-ce que l'on doit regarder aussi le morphisme de Frobénius ?
ce n'est pas pour être méchant (en fait , si), mais si on écrit
un triangle de Pascal modulo 2, avec des 1 et 0, en remplaçant
par leur parité 0-1, on "voit" de jolies choses:
les lignes de rang
les coeff en colonne forment une suite périodique (j'en suis pas si sûr)
j'imagine des relations polynomiales entre les périodes
de suites formées des coefficients d'une colonne.
les lignes d'indice
ça doit être lié à l'exponentiation
est-ce que l'on doit regarder aussi le morphisme de Frobénius ?
voili-voilou le résultat
on regarde l'élévation au carré
^2=1+2x+x^2)
on élève au carré de nouveau
^{2^2} = 1^2+ 4x^2+ x^4 + 2(2x+2x^3+x^2))
modulo 2, les doubles produits comptent pour des prunes.
et les carrés des coefficients de^2) ont même parité
ont même parité
que leur antécedents
d'où par récurrence
^{2^k})
comporte exactement deux coefficients binomiaux impairs. :zen:
ensuite on réduit par congruence de polynômes
(me demande pas de quelle relation d'équivalence , il s'agit!)
^n \equiv (1+x)^{a_k 2^k+a_{k-1} 2^{k-1}+ ..+2 a_1 +a_0})
^n \equiv \Pi (1+x^{2^i}))
le produit étant pris sur les digits a_i, en base 2, non nuls de l'exposant n.
car^2) est congru à
est congru à 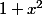
maintenant , on regarde sur un exemple:
exemple:
le produit(1+x^8)(1+x^16)=1+x^2+x^8+x^{10}+x^{16} +x^{18}+x^{24}+x^{26})
on voit donc que chaque facteur donne deux termes de la somme.
on conclue:
dans le développement du binome de^n)
il y a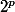 coefficients binomiaux impairs
coefficients binomiaux impairs
où p est le nombre de digits non nuls de l'exposant n, quand l'exposant n est écrit en base 2.
on élève au carré de nouveau
modulo 2, les doubles produits comptent pour des prunes.
et les carrés des coefficients de
que leur antécedents
d'où par récurrence
comporte exactement deux coefficients binomiaux impairs. :zen:
ensuite on réduit par congruence de polynômes
(me demande pas de quelle relation d'équivalence , il s'agit!)
le produit étant pris sur les digits a_i, en base 2, non nuls de l'exposant n.
car
maintenant , on regarde sur un exemple:
exemple:
le produit
on voit donc que chaque facteur donne deux termes de la somme.
on conclue:
dans le développement du binome de
il y a
où p est le nombre de digits non nuls de l'exposant n, quand l'exposant n est écrit en base 2.
Des morphismes, des coordonnées !!
pusep a écrit:Merci beaucoup!!
de rien.
On considère le triangle de Pascal, vaste sujet d'étude et de rêverie depuis Blaise.
On complète par des zéros au dessus de la diagonale de "1" et à droite.
Ce triangle de Pascal, en fait ce quart de plan à coordonnées entières (k,n),
est traversé par de nombreuses applications linéaires, un peu à la
manière,toutes proportions gardées, dont l'espace euclidien est soumis aux endomorphismes.
En autres applications linéaires ou "formules":
i)
on considère l'opérateur de dérivation D sur l'espace des suites à coefficients entiers.
défini par:
D est linéaire et envoie la colonne
sur
car la formule entre coefficients binomiaux
se réécrit
Comme on "dérive" pour passer d'une colonne l'autre, on va donc "primitiver"
on écrit l'opérateur
défini par:
soit
où
Bon, y a un truk qui ne marche pas bien, c'est qu'on intégre
de 0 à (n-1) la suite
il y a un effet de bord.
autre morphisme concernant les lignes
si on pose
on a les formules
et donc les applications
vérifiant la composition
partitionnent l'ensemble des lignes selon des orbites ??
Sont-ce les morphismes de Frobénius ?
L'idée, puisque les lignes du tableau correspondent à des polynômes,
c'est d'obtenir les colonnes (infinies) sous forme de séries génératrices
de manière à symétriser le problème.
Il y a donc des relations entre les exposants des binômes
et leurs coefficients de polynômes, via des opérateurs linéaires.
Le souçi, c'est que les morphismes
dans des corps de nombres adéquats.
Quand aux colonnes
On peut peut être (ré)obtenir des formules en considérant une base
naturelle de ces noyaux.
En tous cas, le but serait d'obtenir:
i) des formules de calcul symbolique
ii) ptet l'écriture en base q
BOn finalement je résume le tout...
On prend P(X) dans Z/2Z[X]
on considère le binôme:
(1+X)^n= SOMME (k parmi n) X^k tel que (k parmi n) est impair (puisque les coefficients pairs seront nuls.
LE cardinale de l'ensemble recherché vaut donc le nombre de monôme dans le dévelloppement de P(X) dans Z/2Z[X]
On décompose n en base 2, ce qui donne :
n= a0 + 2a1 + 2^2a2 + .... + 2^r.ar
(1+X)^n=(1+X)^a0.(1+X)^2a1.....(1+X)^(2^r.ar)
L'ensemble E={i dans {0,...,r} tes que ai=1} est tel que
(1+X)^n=PRODUIT (1+X)^(2^i) dans Z/2Z avec i dans E
DE plus, (1+X)^(2^i)=1+X^(2^i)
et (1+X)^n=PRODUIT (1+X^(2^i))
En développant le tout, ce qui donne au maximum 2^(card E) monômes de la forme (en posant E={j1,....jp} avec p=card E)
X^(b1.2^(j1)).X^(b2.2^(j2)).....X^(bp.2^(jp)) avec bk= 0 ou 1 selon que l'on choisisse 1 ou X^(bk.2^(jk))
Finalement, (1+X)^n= SOMME X^(SOMME bi.2^(ji)) (*) pour bi dans {0;1}
De plus, l'application f:{0;1}^p -> N
(b1...bp) -> SOMME bi.2^(ji) est injective, donc tous les exposants dans (*) sont différents
On a alors card {k dans {0,...,n} (k parmi n) impair } = p
Finalement, ce cardinal correspond exactement au nombre de 1 qui figurent dans la l'écriture binaire de n.
Merci busard_des_roseaux , un exercice très intéressant, mais qui donne du fil à retorde!!!
On prend P(X) dans Z/2Z[X]
on considère le binôme:
(1+X)^n= SOMME (k parmi n) X^k tel que (k parmi n) est impair (puisque les coefficients pairs seront nuls.
LE cardinale de l'ensemble recherché vaut donc le nombre de monôme dans le dévelloppement de P(X) dans Z/2Z[X]
On décompose n en base 2, ce qui donne :
n= a0 + 2a1 + 2^2a2 + .... + 2^r.ar
(1+X)^n=(1+X)^a0.(1+X)^2a1.....(1+X)^(2^r.ar)
L'ensemble E={i dans {0,...,r} tes que ai=1} est tel que
(1+X)^n=PRODUIT (1+X)^(2^i) dans Z/2Z avec i dans E
DE plus, (1+X)^(2^i)=1+X^(2^i)
et (1+X)^n=PRODUIT (1+X^(2^i))
En développant le tout, ce qui donne au maximum 2^(card E) monômes de la forme (en posant E={j1,....jp} avec p=card E)
X^(b1.2^(j1)).X^(b2.2^(j2)).....X^(bp.2^(jp)) avec bk= 0 ou 1 selon que l'on choisisse 1 ou X^(bk.2^(jk))
Finalement, (1+X)^n= SOMME X^(SOMME bi.2^(ji)) (*) pour bi dans {0;1}
De plus, l'application f:{0;1}^p -> N
(b1...bp) -> SOMME bi.2^(ji) est injective, donc tous les exposants dans (*) sont différents
On a alors card {k dans {0,...,n} (k parmi n) impair } = p
Finalement, ce cardinal correspond exactement au nombre de 1 qui figurent dans la l'écriture binaire de n.
Merci busard_des_roseaux , un exercice très intéressant, mais qui donne du fil à retorde!!!
pusep a écrit:un exercice très intéressant
oui, peut être pouvons nous vivre sur la bête encore quelque temps... :zen:
i) la théorie auquel je pensais existe déja.ça s'appelle les entiers de Witt.
:hum:
ii)
j'ai un résultat (prometteur ?? ou trivial ? je ne sais) : en base 2, les colonnes
du triangle de Pascal forment des suites périodiques.
voila l'idée:
on note c_k la suite :
par différence divisée
en itérant k fois l'opérateur:
Si l'on réfléchit à ce qu'est une différence divisée,
ça signifie que la suite c_k (k fixé)
suite de la variable entière n, vérifie une récurrence linéaire d'ordre k.
Son équation caractéristique est
Dans Z:2Z, elle est périodique, de longueur max
iii)
je cherche une série double, sommée sur k et n, d'indéterminée
J'en ai trouvé une dans la littérature,
convient-elle ?
iii)
Remarque:
Quand on veut sommer une série , du style
on peut écrire un x en facteur,
et hop ensuite on intégre une fois,
puis x en facteur,
et on réintégre une fois.
on a donc "transféré" le coefficient
Pour obtenir l'écriture en base Q (Q entier
du coefficient binomial
il s'agirait de transférer ces divisions euclidiennes sur les exposants,
comme on le fait pour les séries entières.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
