Salut,
Pour le premier, il y a une astuce archi classique pour trouver sans effort le nombre de k-uplets
\!\in\! \mathbb{N}^k)
tels que ,
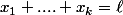
(avec
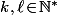
connus) :
Pour représenter une solution du bidule, tu imagine une ligne constituée de "cases" sur laquelle tu commence par laisser

cases vides, puis tu met une marque dans la case suivante, puis

cases vides, puis une marque, etc jusqu'à la dernière marque suivie de
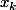
cases vides.
Si tu regarde le dessin final, il est constitué de
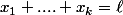
cases vides plus
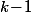
cases avec une marque soit un total de
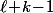
cases. Et si tu as deux sous de bon sens, il est clair que l'ensemble des solutions au problème est en bijection avec l'ensemble des façons de mettre
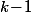
marques sur une ligne de
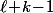
cases donc que le nombre de solutions, c'est le coefficient binomial
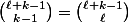
Dans ton cas où
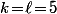
il faut mettre 4 marques sur une ligne de 9 cases et, si par exemple, on les place de cette façon XOOXXOXOO (ou O=case vide) ça correspond à la solution 0+2+0+1+2 = 5