Ensemble fini et cardinal
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Juil 2019, 01:16
par mehdi-128 » 11 Juil 2019, 01:16
Bonsoir,
Je ne comprends absolument rien à cet exercice ni à la correction de mon livre qui est du chinois.
Soit

un ensemble fini de cardinal

et

une bijection de
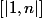
sur

. Si

est un élément de

, construire une bijection

de
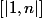
sur

telle que
=a)
. En déduire que
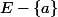
est fini et de cardinal

.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 11 Juil 2019, 06:23
par GaBuZoMeu » 11 Juil 2019, 06:23
mon livre qui est du chinois.
Garde-toi de ce genre de jugement, et demande-toi si tu n'es pas le premier responsable de ton incompréhension. Au vu de ce que tu nous as montré jusqu'à présent ...
Si la bijection

qui t'est donnée envoie

sur

, il n'y a rien à faire.
Si elle envoie

sur
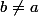
, que faire pour la modifier afin d'obtenir le résultat voulu (que l'image de

soit

) ? Peut-être échanger

et

, non ?
Essaie de visualiser la situation sans te noyer dans le formalisme. Une fois la situation (simple !) bien comprise, la formalisation vient aisément.
-
aviateur
 par aviateur » 11 Juil 2019, 07:57
par aviateur » 11 Juil 2019, 07:57
Bonjour
On est tombé sur la tête ici ou quoi?
On a un ensemble E contenant n éléments (n plus grand ou égal à 1). On lui retire l'élément a. Montrer qu'il reste n-1 éléments.
C'est un exercice d'école maternelle version moderne:
Un enfant a 4 bonbons mais il en mange 1. Combien en reste-t-il?
Indication: Utiliser une bijection.
N'y a -t-il pas des exercices sur la cardinalité plus intéressant?
Modifié en dernier par aviateur le 11 Juil 2019, 14:09, modifié 1 fois.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 11 Juil 2019, 10:13
par capitaine nuggets » 11 Juil 2019, 10:13
Salut !
mehdi-128 a écrit:Je ne comprends absolument rien à cet exercice ni à la correction de mon livre qui est du chinois.
Je croyais que ton livre était "très bien fait" et maintenant c'est du chinois ?
aviateur a écrit:N'y a -t-il pas des exercices sur la cardinalité plus intéressant?
Apparement il veut des réponses à ces questions : la plupart de ses discussions postées ici sur le forum le sont aussi sur ilemaths. Du coup, est-ce que c'est vraiment la peine de lui répondre ? D'autres lui donneront exactement les même réponses, je passe la main sur ce coup là.

-
noobey
- Membre Naturel
- Messages: 41
- Enregistré le: 17 Avr 2019, 15:51
-
 par noobey » 11 Juil 2019, 12:02
par noobey » 11 Juil 2019, 12:02
Jpense quau lieu de faire des maths il devrait travailler dans le recopiage de bouquins vu que cest son activité favorie
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Juil 2019, 14:34
par mehdi-128 » 11 Juil 2019, 14:34
capitaine nuggets a écrit:Salut !
mehdi-128 a écrit:Je ne comprends absolument rien à cet exercice ni à la correction de mon livre qui est du chinois.
Je croyais que ton livre était "très bien fait" et maintenant c'est du chinois ?
aviateur a écrit:N'y a -t-il pas des exercices sur la cardinalité plus intéressant?
Apparement il veut des réponses à ces questions : la plupart de ses discussions postées ici sur le forum le sont aussi sur ilemaths. Du coup, est-ce que c'est vraiment la peine de lui répondre ? D'autres lui donneront exactement les même réponses, je passe la main sur ce coup là.

Je n'ai pas posté cet exercice sur l’île des maths. Je vais vous mettre la correction de mon livre et vous allez comprendre pourquoi je dis ça.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 11 Juil 2019, 15:04
par capitaine nuggets » 11 Juil 2019, 15:04
Oui sans vouloir être désagréable, comment veux-tu te concentrer et prendre le temps de chercher un exo comme il faudrait alors que tu en postes trois ou quatre par jours ? Chercher un exo demande du temps et de la réflexion, ça ne se fait pas toujours en cinq minutes. Je me demande d'ailleurs si tu arrives à retenir quelque chose de tous les exos que tu postes tous les jours. Surtout si tu as d'autres occupations dans la vie en dehors des maths, pire si tu travailles. Parce que ce n'est pas évident.
Ensuite, la correction m'importe peu. Dans ce type de livre, elle est plus censé fournir des éléments de réponse qu'un corrigé détaillé (n'espère pas qu'un livre de ce volume puisse corriger complètement tous les exos, il est déjà assez gros comme ça). Perso, je préfère privilégier les livres thématiques plutôt que les livres tout-en-un. Soit ils ont peu/pas d'exos, soit ils font de courtes démonstrations. Enfin, je trouve en général les livres thématiques plus complet et mieux écrit que les livres "tout-en-un" souvent purement scolaire.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Juil 2019, 15:07
par mehdi-128 » 11 Juil 2019, 15:07
@GaBuZoMeu
Merci j'ai compris en utilisant un exemple simple :
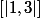
sur
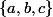
.
La correction du livre est assez technique ça m'a fait peur, mais vous avez raison, il vaut mieux raisonner sans formalisme pour commencer !
Si

, on a
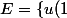 \} = \{a\})
. Ainsi
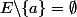
et
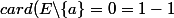
Supposons

.
Si
=a)
, alors

étant bijective,
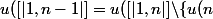 \} = E \backslash \{a \})
Par suite, l'application
)
est surjective. Elle est aussi injective comme restriction d'une injection.
Ainsi

est bijective et
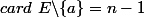
Si
 \ne a)
considérons l'application

définie par :
=u(n))
,
)=a)
et
=x)
C'est une permutation involutive de

puisque
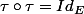
. Par suite
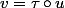
est une bijection de
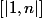
sur

, composée de 2 bijections vérifiant
=\tau(v(n))=a)
.
D'après le premier cas, on en déduit que :
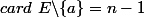
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Juil 2019, 15:12
par mehdi-128 » 11 Juil 2019, 15:12
C'est un exercice intégré dans le cours donc la démonstration est détaillée. Mais je la trouve trop formelle.
Les livres "scolaires" sont plus adaptés à mon niveau et mon objectif. Je voulais un livre avec tout le cours de 1ère année et toutes les démonstrations détaillées, c'est le seul que j'ai trouvé.
Je suis en vacances, je suis professeur contractuel, donc j'ai un peu plus de temps. Mais cette année j'ai essayé de travailler les maths en parallèle de mon travail ce qui n'est pas évident. J'ai pu travailler 7 chapitres :
Droite numérique, fonctions à valeurs réelles.
Calculs algébriques.
Nombres complexes.
Fonctions usuelles.
Primitives et équations différentielles linéaires.
Raisonnements, opérations sur les ensembles.
Et le je suis à la fin du chapitre assez difficile : applications, relations, entiers naturels.
-
aviateur
 par aviateur » 11 Juil 2019, 15:58
par aviateur » 11 Juil 2019, 15:58
mehdi-128 a écrit:Je suis en vacances, je suis professeur contractuel, donc j'ai un peu plus de temps..
Tu enseignes quelle matière?
-
aviateur
 par aviateur » 11 Juil 2019, 16:07
par aviateur » 11 Juil 2019, 16:07
mehdi-128 a écrit:@GaBuZoMeu
Merci j'ai compris en utilisant un exemple simple :
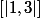
sur
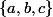
.
La correction du livre est assez technique ça m'a fait peur, mais vous avez raison, il vaut mieux raisonner sans formalisme pour commencer !
Si

, on a
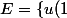 \} = \{a\})
. Ainsi
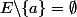
et
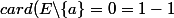
Supposons

.
Si
=a)
, alors

étant bijective,
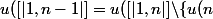 \} = E \backslash \{a \})
Par suite, l'application
)
est surjective. Elle est aussi injective comme restriction d'une injection.
Ainsi

est bijective et
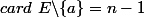
Si
 \ne a)
considérons l'application

définie par :
=u(n))
,
)=a)
et
=x)
C'est une permutation involutive de

puisque
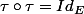
. Par suite
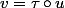
est une bijection de
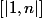
sur

, composée de 2 bijections vérifiant
=\tau(v(n))=a)
.
D'après le premier cas, on en déduit que :
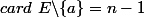
Tout ça pour montrer que si E est de cardinal fini et si
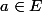
alors
 =card(E)-1.)



Utiliser la notion de bijection, surjection, de permutation involutive,
Fallait y penser!
Mais je ne sais pas si ça va motiver à faire des études de math dans le supérieur.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 12 Juil 2019, 16:36
par mehdi-128 » 12 Juil 2019, 16:36
Après réflexion, c'est pas si compliqué. Il suffit de permuter 2 éléments, la fonction tau est simple quand on a compris le principe.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
sur
.
, on a
. Ainsi
et
.
, alors
étant bijective,
est surjective. Elle est aussi injective comme restriction d'une injection.
est bijective et
considérons l'application
définie par :
,
et
puisque
. Par suite
est une bijection de
sur
, composée de 2 bijections vérifiant
.