Cardinal d'ensemble et demonstration

[yoshiop]

bonjour

je bloque sur une démonstration à faire :

a) soient E et F deux ensembles finis et
b) soient E X F finis et
c) l'ensemble f(E,F) est finis (f^card(E))

il faut démontrer a) b) c) par récurrence et je ne vois pas du tout comment commencer vus que c'est des ensembles ..;
pouvez vous m'aider svp

merci

[infernaleur]

Salut,
tu peux procéder par récurrence sur n=card(E).

[tournesol]

La rédaction me parait difficile .
Pour le 1 je propose ceci:
soit n le cardinal de E
je note A(n) le cardinal de EUF , et B(n) l'entier card(E)+card(F)-card(E inter F)
tu dois vérifier que A(0)=B(0)
supposons A(n)=B(n)
Si on adjoint à E un élement supplémentaire x , alors :
A(n) augmente d'une unité .
si x appartient à (E inter F) , B(n) augmente de 1+1-1=1
donc A(n+1)=B(n+1)
si x n'appartient pas à (E inter F) , ...

[tournesol]

notons que sans recurrence , 1 est facile :
card(EUF)=card(E\F)+card(E inter F)+card(F\E)=(card(E\F)+card(E inter F))+(card(F\E)+ card(E inter F))-card(E inter F)=card(E)+card(F)-card(E inter F)

[tournesol]

je réfute ma rédaction par récurrence.
En effet l'hypothèse de récurrence est absente .

[tournesol]

je ne traiterai pas cet exo car les solutions sont dépendantes des définitions des cardinaux données en cours .
Au secours les autres !

[infernaleur]

1)on montre que pour E et F disjoint et on en déduit la cas général avec ce qu'a dit tournesol .

Soit F un ensemble finis et on pose card(F)=p
On pose n=card(E)

Initialisation: pour n=0 c'est évident

Hérédité: on suppose que pour tout ensemble A avec et .
Montrons que

Comme on a une bijection
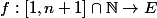
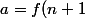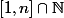
En posant , la restriction de f à donne une bijection .
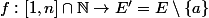
Comme par hypothèse de récurrence on a .
On a donc une bijection .
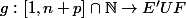
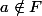
Comme E et F sont disjoints, on a forcément donc
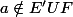
Donc en posant on obtient une bijection
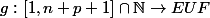
D’où