Caractérisation sequentielle des points adhérents.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 18 Avr 2012, 11:43
par Rifl3 » 18 Avr 2012, 11:43
Bonjour je voudrait montrer cette caractérisation dans un ensemble A inclus dans un Kevn E (A C E),aE
alors aAdh(A) ssi il existe au moins une suite (xn) d'éléments de A, de limite a.
J'arrive a démontrer le sens auriez vous une idée svp?
Ceci en se ramenant à la def :
 \Leftrightarrow \forall r>0,A\cap B_{f}(a,r)\neq \emptyset)
Merci beaucoup.

-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 18 Avr 2012, 12:43
par ev85 » 18 Avr 2012, 12:43
Rifl3 a écrit:Bonjour je voudrait montrer cette caractérisation dans un ensemble A inclus dans un Kevn E (A C E),aE
alors aAdh(A) ssi il existe au moins une suite (xn) d'éléments de A, de limite a.
J'arrive a démontrer le sens auriez vous une idée svp?
Ceci en se ramenant à la def :
 \Leftrightarrow \forall r>0,A\cap B_{f}(a,r)\neq \emptyset)
Merci beaucoup.

Tu prends des boules de rayons
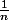
.
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 18 Avr 2012, 13:18
par Rifl3 » 18 Avr 2012, 13:18
ev85 a écrit:Tu prends des boules de rayons
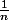
.
Ok, merci. J'ai réussi à bien le rédiger et le mettre en forme.

Sinon j'ai une autre question :
J'avais une question ou je devait montrer que
dt)
est de classe C1.
Et
la question suivante est trouver une équation différentielle linéaire d'ordre 1 dont f soit solution.
Mais je ne vois pas trop, par exemple si je dis que l'equadiff est
}{x}+f(x)=\int_0^{+\infty} exp{-t^2+ixt}dt)
C'est bon??? Dans ce cas on peut trouver beaucoup d'équadiffs que f vérifie non?
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 18 Avr 2012, 13:32
par ev85 » 18 Avr 2012, 13:32
Rifl3 a écrit: la question suivante est trouver une équation différentielle linéaire d'ordre 1 dont f soit solution.
Mais je ne vois pas trop, par exemple si je dis que l'equadiff est
}{t}+f(t)=\int_0^{+\infty} exp{-t^2+ixt}dt)
C'est bon???
Je n'ai pas vérifié mais ton choix de variable (t) est hautement suspect.
Rifl3 a écrit:Dans ce cas on peut trouver beaucoup d'équadiffs que f vérifie non?
Oui bien entendu. f est solution de
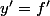
ou de

pour fixer les idées...
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 18 Avr 2012, 13:44
par Rifl3 » 18 Avr 2012, 13:44
Oui desolé je voulais dire x. J'ai changé :)
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 18 Avr 2012, 14:13
par ev85 » 18 Avr 2012, 14:13
Rifl3 a écrit:Oui desolé je voulais dire x. J'ai changé

 = \int_0^{+\infty} \exp(-t^2+itx)\,dt)
 = \int_0^{+\infty} it\exp(-t^2+itx)\,dt)
Tu intègres par parties en primitivant
)
.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 19 Avr 2012, 20:50
par Judoboy » 19 Avr 2012, 20:50
Au passage, est-ce qu'on a une caractérisation séquentielle ou un équivalent pour les espaces topologiques ? j'ai tendance à penser que non à cause des bases de voisinages éventuellement non dénombrables, mais est-ce qu'on a quelque chose qui se rapproche avec les filtres ou pas ?
D'ailleurs si quelqu'un a un exemple de base de voisinages non dénombrable, j'arrive pas à en imaginer une (peut-être parce qu'on bosse en pratique 99% du temps sur des espaces métriques)...
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 21 Avr 2012, 01:21
par Judoboy » 21 Avr 2012, 01:21
Heuppe. (pas moins de 10 caractères -.-)
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 21 Avr 2012, 08:04
par ev85 » 21 Avr 2012, 08:04
Judoboy a écrit:Heuppe. (pas moins de 10 caractères -.-)
Regarde du côté de la topologie faible (hors dimension finie bien sûr)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
.
C'est bon???