allmess a écrit:Merci pour vos réponses,
En se plaçant dans
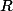
, un sous ensemble A est dit ouvert pour la norme N si
\subset A)
,
oui
autrement dit
$, $N(x-a)<r$)
.
Non alors déjà tu ne remplaces pas un

qui est un symbole mathématique, par un mot français "soit".
Les mots français tu les utilises quand tu fais des phrases en français, tu ne les mets pas au milieu des formules de maths.
Aussi j'avais pas remarqué mais soit tu as renommé le a en x (pour parler d'un autre a plus tard, c'est quand même pas génial d'échanger les noms des gens sans prévenir), soit tu as décidé de complètement inverser l'ordre de tout le monde sans raison. (et c'est encore pire parceque là tu peux être certain que tu vas dire n'importe quoi)
Ensuite, "r>0" là aucun quantificateur donc j'imagine que tu voulais aussi dire "soit r>0", donc tu as transformé un
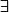
en

, va savoir pourquoi.
Ensuite tu t'es planté dans la défintion de "machin est inclus dans truc".
"machin est inclus dans truc" ça veut dire "pour tout x dans machin, x est dans truc".
Toi, j'ai l'impression que tu as dit "pour tout x dans machin, x est dans machin".
("pour tout x dans la boule ouverte de centre a et de rayon R, N(x-a) < R").
Certes c'est la définition de boule ouverte mais ça n'a rien à faire là comme tu l'as mis.
 \subset A)
on remplace "inclus dans" par sa définition :
, a \in A)
on remplace
)
par sa définition (un élément de la boule dans R de centre x de rayon r pour la norme N, c'est un élément a de R tel que N(x-a)<r)
<r \implies a \in A))
