Calcul d'une matrice à n lignes et n colonnes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Swayf
- Messages: 8
- Enregistré le: 27 Mai 2018, 12:07
-
 par Swayf » 31 Mai 2018, 18:14
par Swayf » 31 Mai 2018, 18:14
Bonsoir,
Je m'en remets à vous pour essayer de comprendre comment il faut faire avec ce genre de matrices "très longues".
La matrice est la suivante que l'on appellera A : ( 2 1 1 1 ... 1)
(1 2 1 1.....1)
(1 1 2 1.....1)
(1...2 1.......1)
(1...............2)
Voici à quoi ressemble la matrice à l'aide d'une capture d'écran :

Il s'agira alors de calculer en premiers temps : A²-(n+2)*A+(n+1)*I et dans un second temps d'inverser la matrice (grâce à A et I) mais je dois avouer que comme la matrice n'est pas finie, je n'ai aucune idée de comment je dois faire, à moins que je doive passer par des lettres

Je vous remercie par avance et vous souhaite une excellente soirée !

-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 31 Mai 2018, 18:28
par Pseuda » 31 Mai 2018, 18:28
Bonsoir,
Tu peux poser
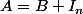
, avec

matrice composée que de

.
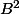
est facilement calculable ...
-
Swayf
- Messages: 8
- Enregistré le: 27 Mai 2018, 12:07
-
 par Swayf » 31 Mai 2018, 19:03
par Swayf » 31 Mai 2018, 19:03
Pseuda a écrit:Bonsoir,
Tu peux poser
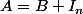
, avec

matrice composée que de

.
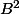
est facilement calculable ...
Merci beaucoup pour votre réponse. Je comprends parfaitement le raisonnement mais je vous avoue ne pas savoir quoi faire après

.. C'est justement parce que j'ai beaucoup de difficultés sur ce type d'exercices que je me permets de vous demander votre aide en espérant mieux comprendre..
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 31 Mai 2018, 19:07
par Pseuda » 31 Mai 2018, 19:07
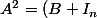^2= B^2 + ... ?)
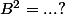
. Commence à t'entraîner avec n=2, n=3, ...
-
Swayf
- Messages: 8
- Enregistré le: 27 Mai 2018, 12:07
-
 par Swayf » 31 Mai 2018, 20:45
par Swayf » 31 Mai 2018, 20:45
Pseuda a écrit: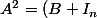^2= B^2 + ... ?)
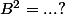
. Commence à t'entraîner avec n=2, n=3, ...
A² = I + n*B + n(n-1)/2 * B² (d'après le binôme de Newton car la condition B*I est validée), est-ce ce que je devais trouver ?
Merci énormément encore pour votre réponse !
-
aviateur
 par aviateur » 01 Juin 2018, 07:45
par aviateur » 01 Juin 2018, 07:45
Bonjour
On peut aussi trouver le polynôme annulateur de A de la façon suivante.
C'est clair que 1 est valeur propre d'ordre (n-1) (voir que B est de rang 1) et en utilisant la trace de A la seconde valeur propre est n+1.
De plus (la matrice A étant symétrique donc diagonalisable) on en déduit que le polynôme annulateur de + bas degré (i;e le polynôme minimal) est :
(z-(n+1))=z^2 -(n+2)z +n+1.)
On a bien
A+(n+1)I=0)
d'où le calcul de

-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 01 Juin 2018, 09:40
par Pseuda » 01 Juin 2018, 09:40
Swayf a écrit: Pseuda a écrit: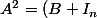^2= B^2 + ... ?)
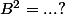
. Commence à t'entraîner avec n=2, n=3, ...
A² = I + n*B + n(n-1)/2 * B² (d'après le binôme de Newton car la condition B*I est validée), est-ce ce que je devais trouver ?
Merci énormément encore pour votre réponse !
Bonjour,
Ouh là, joyeux mélange.
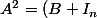^2= B^2 + 2 B I_n + I_n^2=B^2 + 2 B + I_n)
.
Prends

.
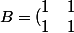)
.
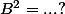
. Fais-le aussi avec n=3.
De manière générale pour

quelconque, on voit que :
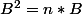
. Donc
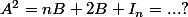
. Prends cette expression pour la mettre dans l'autre.
à continuer ...
-
Swayf
- Messages: 8
- Enregistré le: 27 Mai 2018, 12:07
-
 par Swayf » 01 Juin 2018, 14:07
par Swayf » 01 Juin 2018, 14:07
aviateur a écrit:Bonjour
On peut aussi trouver le polynôme annulateur de A de la façon suivante.
C'est clair que 1 est valeur propre d'ordre (n-1) (voir que B est de rang 1) et en utilisant la trace de A la seconde valeur propre est n+1.
De plus (la matrice A étant symétrique donc diagonalisable) on en déduit que le polynôme annulateur de + bas degré (i;e le polynôme minimal) est :
(z-(n+1))=z^2 -(n+2)z +n+1.)
On a bien
A+(n+1)I=0)
d'où le calcul de

Bonjour,
Je vois mais comment démontrer que c'est bien un polynôme annulateur de la matrice, ça me paraît quelque peu délicat..
-
Swayf
- Messages: 8
- Enregistré le: 27 Mai 2018, 12:07
-
 par Swayf » 01 Juin 2018, 14:11
par Swayf » 01 Juin 2018, 14:11
Pseuda a écrit: Swayf a écrit: Pseuda a écrit: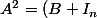^2= B^2 + ... ?)
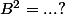
. Commence à t'entraîner avec n=2, n=3, ...
A² = I + n*B + n(n-1)/2 * B² (d'après le binôme de Newton car la condition B*I est validée), est-ce ce que je devais trouver ?
Merci énormément encore pour votre réponse !
Bonjour,
Ouh là, joyeux mélange.
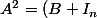^2= B^2 + 2 B I_n + I_n^2=B^2 + 2 B + I_n)
.
Prends

.
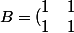)
.
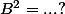
. Fais-le aussi avec n=3.
De manière générale pour

quelconque, on voit que :
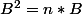
. Donc
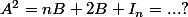
. Prends cette expression pour la mettre dans l'autre.
à continuer ...
Veuillez m'excuser pour mon erreur, j'ai l'habitude de travailler sur des matrices à la puissance n et je me suis un peu emmêlé les pinceaux... Je viens de comprendre, merci beaucoup pour votre aide !!
Je vous souhaite une excellente journée

-
aviateur
 par aviateur » 01 Juin 2018, 14:47
par aviateur » 01 Juin 2018, 14:47
Swayf a écrit: aviateur a écrit:Je vois mais comment démontrer que c'est bien un polynôme annulateur de la matrice, ça me paraît quelque peu délicat..
Rebonjour, je ne vois rien de délicat ici et c'est même la substantifique moelle des matrices.
La matrice diagonale semblable est
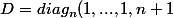)
est c'est facile de voir que
(D-(n+1) I)=0)
. Il en est de même pour l'endomorphisme sous-jacent donc pour A aussi.
Evidemment on peut faire comme @pseuda a indiqué mais il y a apprendre dans ma solution.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités


