Bonjour à tous
J'aurai besoin d'aide concernant le calcul de surface (aire) de polygones complexes
Par exemple un polygone avec N cotés
le premier coté N1 de longuer X et d'angle y°
le 2ème coté N2 de longueur x1 et d'angle y2°
ainsi de suite .....
Connaitriez vous une formule mathématique qui me permette de calculer la surface connaissant le nombre de coté, leur longueur et leur angles, là c trop chaud pour moi je me suis arrété au lycée et a moins de tout décortiquer en surface conventionnelle type triangle et carré je vois pas ....
Merci à ceux qui pourront m'aider ( c pour une application concrete : calcul de superficie des champs agricole au Mali)
Calcul de surface de polygone complexe
5 messages
- Page 1 sur 1
MatosBKO a écrit:Bonjour à tous
J'aurai besoin d'aide concernant le calcul de surface (aire) de polygones complexes
Par exemple un polygone avec N cotés
le premier coté N1 de longuer X et d'angle y°
le 2ème coté N2 de longueur x1 et d'angle y2°
ainsi de suite .....
Connaitriez vous une formule mathématique qui me permette de calculer la surface connaissant le nombre de coté, leur longueur et leur angles, là c trop chaud pour moi je me suis arrété au lycée et a moins de tout décortiquer en surface conventionnelle type triangle et carré je vois pas ....
Merci à ceux qui pourront m'aider ( c pour une application concrete : calcul de superficie des champs agricole au Mali)
Tu veux sûrement calculer d'un polygone non régulier. Moi, je cherche le centre circonscrit de ces polygones :ptdr:
Il faut sûrement découper ton polygone en plus petit polygone dont on connait la surface....
je sais pas si ça pourrait aider j'ai un programme sur une calculette sharp qui calcule cela mais je comprend pas les formule de math et je voudrais reprogrammer ce prog sur une casio, faudrait d'abord que je comprenne voila le prog ci dessous
je comprend rien y a des variable partout non préalablement définis
voilà le prog sur sharp
10 : "A" : PAUSE "CALCUL DE SUPERFICIE"
20 : CLEAR : INPUT "NOMBRE DE COTE =" ; N
30 : FOR I = 1TO N : PAUSE "........." . I
40 : INPUT " ANGLE= " ; A , "COTE=" ; B
50 : P=P+B : X= X+B* SIN A : Y = Y+B*COS A
60 : W = W+X : Z=Z+Y
70 : S = S+B*SIN A * Y - B*COS A * X
80 : NEXT I
90 : C = (racine carré) ( X*X + Y*Y)/P*100 : IF C >5 GOTO 130
100 : S = ABS( S/2+Y*W/N-X*Z/N)/100+5
110 : PRINT USING "####" ; "S =" ; S; "ARES"
120 : GOTO 20
130 : PRINT " MESURE A REPRENDRE"
140 : GOTO 20
150 : END
Voilà j'espère que j'ai pas taper tout ça pour rien :cry:
je comprend rien y a des variable partout non préalablement définis
voilà le prog sur sharp
10 : "A" : PAUSE "CALCUL DE SUPERFICIE"
20 : CLEAR : INPUT "NOMBRE DE COTE =" ; N
30 : FOR I = 1TO N : PAUSE "........." . I
40 : INPUT " ANGLE= " ; A , "COTE=" ; B
50 : P=P+B : X= X+B* SIN A : Y = Y+B*COS A
60 : W = W+X : Z=Z+Y
70 : S = S+B*SIN A * Y - B*COS A * X
80 : NEXT I
90 : C = (racine carré) ( X*X + Y*Y)/P*100 : IF C >5 GOTO 130
100 : S = ABS( S/2+Y*W/N-X*Z/N)/100+5
110 : PRINT USING "####" ; "S =" ; S; "ARES"
120 : GOTO 20
130 : PRINT " MESURE A REPRENDRE"
140 : GOTO 20
150 : END
Voilà j'espère que j'ai pas taper tout ça pour rien :cry:
Salut,
j'ai l'impression que ce programme calcule l'aire de polygones convexes (cad sans angle rentrant).
L'idée est la suivante :
Le calcul des coordonnées se fait de proche en proche :
Soit les sommets.
les sommets. 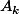 a pour coordonnées
a pour coordonnées ) l'angle correspondant est
l'angle correspondant est  la longueur du coté
la longueur du coté  est
est 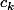 on a besoin de "l'inclinaison"
on a besoin de "l'inclinaison" 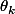 du coté
du coté  .
.
On a alors (avec des angles en degré)
\\<br />x_k= x_{k-1}+c_k\cos\theta_k\\<br />y_k= y_{k-1}+c_k\sin\theta_k)
On peut remarquer qu'il est inutile de conserver la liste des coordonnées, on calcule le point suivant et l'aire du triangle correspondant et on l'ajoute à l'aire déjà calculée.
Enfin on peut vérifier que le polygone se referme effectivement.
j'ai l'impression que ce programme calcule l'aire de polygones convexes (cad sans angle rentrant).
L'idée est la suivante :
- Si on connait les coordonnées des sommets d'un triangle il est facile de calculer son aire avec le déterminant de 2 cotés. Pour être plus précis l'aire du triangle OAB avec O de coordonnées(0,0)
est égale à
- On divise en suite le polygone en triangles avec les diagonales issues du premier sommet.
- On calcule les coordonnées des sommets dans un repère dont l'origine est le premier sommet (raison pour la quelle j'ai donné la formule de l'aire d'un triangle dans ce cas particulier) et dont l'axe des abscisses est donné par le premier coté.
Le calcul des coordonnées se fait de proche en proche :
Soit
On a alors (avec des angles en degré)
On peut remarquer qu'il est inutile de conserver la liste des coordonnées, on calcule le point suivant et l'aire du triangle correspondant et on l'ajoute à l'aire déjà calculée.
Enfin on peut vérifier que le polygone se referme effectivement.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
