Calcul de norme subordonnée

[yoo]

bonsoir , je suis en train de faire un problème de topologie et je bloque sur la question suivante quelqu'un peut m'aider s'i vous plaît . voici l'énoncé :http://img189.imageshack.us/i/numrisation0003mh.jpg/
merci d'avance

[girdav]

Bonjour,
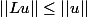
vois-tu pourquoi ? En déduis-tu une inégalité sur la norme subordonnée? Vois-tu comment obtenir l'autre?

[yoo]

pour montrer cette inégalité j'ai essayé de démontrer que :http://img408.imageshack.us/i/numrisation0004p.jpg/ mais je n'arrive pas

[girdav]

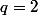
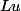
C'est normal, ça ne marche pas puisque si par exemple et on prend la suite qui vaut au terme et pour tous les autres () alors est la suite nulle tandis que la norme de vaut .

[yoo]

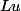
alors est la suite nulle tandis que la norme de vaut .[/quote] . je ne vois pas où est le problème ? on a l'inégalité dans le bon sens

[girdav]

Je n'avais pas vu la constante...
Sinon, on peut se servir du fait que .

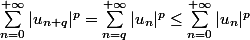
[yoo]

voilà ce que j'ai trouvé mais je ne vois pas pourquoi on a l'inégalité dans l'autre sens ni la justification de la première inégalité pour conclure que norme sub est égale à 1
http://img811.imageshack.us/i/numrisation0005k.jpg/

[girdav]

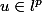
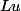
On peut trouver un élément de norme tel que est de norme .

[yoo]

x(n)=(0,.....,0,1,0,.......) le 1 à la n ieme place ca marche je crois

[girdav]

Tu veux dire à la -ième? Oui, ça marche.

[yoo]

oui à la q-ième . merci encore une fois