Bonsoir,
Pour montrer l'axiome de séparation pour la norme subordonnée telle que [TEX]\forall A \in \mathcal{M}_n(\mathbb{R}),\, |||A|||=\sup_{x\in\mathbb{R}^n,||x||1, on est assuré que x ne peut être le vecteur nul, donc il reste à le diviser par sa norme pour obtenir un vecteur unitaire et on montre qu'alors A est nulle par l'argument précédent. Mais c'est justement sur ce dernier résultat que je bloque !
Merci d'avance.
Norme subordonnée.
6 messages
- Page 1 sur 1
Rappel (sous forme de... piqûre) :
Une matrice, ça correspond à une application linéaire et, en particulier,=\lambda A.X) ce qui signifie que, si tu connait la valeur en un vecteur donné, tu en déduit la valeur sur toute la droite vectorielle engendré par le vecteur.
ce qui signifie que, si tu connait la valeur en un vecteur donné, tu en déduit la valeur sur toute la droite vectorielle engendré par le vecteur.
De façon plus générale, dés que tu connait les valeurs que prend une application linéaire sur une base, tu la connait partout et là, tu connait A.X pour l'ensemble des vecteurs X de norme <1 : ça te fournit BIEN PLUS d'info que ce qu'il t'en faut pour conclure...
P.S. c'est d'ailleur du fait que A est linéaire que la "norme subordonnée", on peut, si on préfère, la définir par
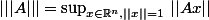
ou bien
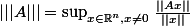
Et, perso, j'ai une préférence pour la dernière qui dit, par définition, que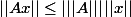 pour toute A et tout x.
pour toute A et tout x.
Une matrice, ça correspond à une application linéaire et, en particulier,
De façon plus générale, dés que tu connait les valeurs que prend une application linéaire sur une base, tu la connait partout et là, tu connait A.X pour l'ensemble des vecteurs X de norme <1 : ça te fournit BIEN PLUS d'info que ce qu'il t'en faut pour conclure...
P.S. c'est d'ailleur du fait que A est linéaire que la "norme subordonnée", on peut, si on préfère, la définir par
ou bien
Et, perso, j'ai une préférence pour la dernière qui dit, par définition, que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Rappel (sous forme de... piqûre) :
Une matrice, ça correspond à une application linéaire et, en particulier,ce qui signifie que, si tu connait la valeur en un vecteur donné, tu en déduit la valeur sur toute la droite vectorielle engendré par le vecteur.
De façon plus générale, dés que tu connait les valeurs que prend une application linéaire sur une base, tu la connait partout et là, tu connait A.X pour l'ensemble des vecteurs X de norme <1 : ça te fournit BIEN PLUS d'info que ce qu'il t'en faut pour conclure...
P.S. c'est d'ailleur du fait que A est linéaire que la "norme subordonnée", on peut, si on préfère, la définir par
ou bien
Et, perso, j'ai une préférence pour la dernière qui dit, par définition, quepour toute A et tout x.
D'accord.
D'ailleurs oui j'aime bien aussi cette dernière définition vu que ça m'aide à montrer que
Ok, j'ai compris en quoi démontrer la ppté pour tout vecteur dans la boule fermée m'aide à le montrer pour tout autre vecteur de R^n. Par contre, le montrer (que si |||A|||=0_K alors A=0_E) dans ce cas, je vois pas trop, du moins avec cette écriture qui me bloque. Si je prends la deuxième écriture (ou la troisième, d'ailleurs) par exemple, elle me dit que le sup est pris parmi tout vecteur de norme exactement égale à 1 (resp' x différent de 0), ce qui m'assure qu'aucun de ces vecteurs n'est nul et donc je montre confortablement que si Ax=0 alors A vaut 0. Peut-être que c'est un abus et que je passe à côté de qqchose d'évident, mais ça me bloque dans le cas présent : Dans la condition où ||x||<1, je peux avoir x=0...
A mon avis, le tout premir truc à faire avec cette "norme subordonnée", c'est de montrer que les sois disant 3 définition sont bien les mêmes et ça provient uniquement du fait que =\lambda A.x)
Donc, partant (par exemple) de ta définition, tu dit que ton sup sur les x de R^n tels que ||x||<1 de ||Ax||, c'est le sup sur les y de R^n tels que ||y||=1 et sur les lambda de [0,1[ de ||A(lambda.y)|| et tu en déduit que c'est la même chose que le sup sur y de R^n tels que ||y||=1 de ||A(y)||. (vu que le sup de lambda.constante pour lambda dans [0,1[, c'est la constante...)
Idem partant de la dernière définition sauf que le lambda disparait complètement du truc dont on cherche le sup...
Donc, partant (par exemple) de ta définition, tu dit que ton sup sur les x de R^n tels que ||x||<1 de ||Ax||, c'est le sup sur les y de R^n tels que ||y||=1 et sur les lambda de [0,1[ de ||A(lambda.y)|| et tu en déduit que c'est la même chose que le sup sur y de R^n tels que ||y||=1 de ||A(y)||. (vu que le sup de lambda.constante pour lambda dans [0,1[, c'est la constante...)
Idem partant de la dernière définition sauf que le lambda disparait complètement du truc dont on cherche le sup...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Sourire_banane a écrit:Bonsoir,
Pour montrer l'axiome de séparation pour la norme subordonnée telle que...
D'après la définition adoptée on a
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
