Calcul Integral

[Alpha77]

Bonjour, je suis en L3 Maths et suite à plusieurs problèmes posés par mon prof de calcul integral et dont deux que je n'arrive pas a résoudre je me tourne vers vous pour de l'aide...

1) On définit A1, ..., An comme des parties d'un ensemble X et appartenant a une tribu A. On me demande de créer une partition finie (B1, ..., Bm) telle qu'on puisse exprimer chaque Ai comme réunion de Bi. J'ai essayé avec Bi=Ai\ U Ak (k=1, i-1) mais on obtient que l'union des Bi égale a An et non pas X comme le recquiert la définition d'une partition.

2) ensuite, on définit ¥ comme étant la mesure de Lebesgue. Soit u la fonction Max (x(1-x), -x(1+x)). On me demande d'exprimer la mesure image de ¥ par rapport a u. Donc comment faire pour calculer la réciproque de u?

Merci d'avance pour l'aide que vous m'apporterez. :we:

[Ben314]

Salut,
Pour le 1, perso, je me ferait pas c... : je considérerais tout ce qui peut s'écrire avec ou bien .
Ca donne ensembles qui forment clairement une partition de X et avec lesquels on peut facilement "reconstituer" les Ai (fait un dessin avec n=3 si tu voit pas trop de quoi je parle).

Pour la 2), tu risque pas de calculer "la réciproque de u" vu que l'application u n'est pas bijective.
Aprés, la question n'est pas super claire : il faut donner quoi comme réponse ? quel calcul permet d'avoir la mesure d'une borélien quelconque (donc en fait juste la définition de la mesure image) ou bien donner la mesure d'un intervalle quelconque (qui permet de retrouver la mesure en question) ?
Perso, j'opterais pour la 2em solution donc j'exprimerais (en fonction de a et b) la mesure d'un intervalle [a,b].

[Alpha77]

Salut Ben,

1) J'avais justement essayé avec http://www.maths-forum.com/images/latex/992d64352bf058e3df9a013f2f7f8304.gif mais on a que l'intersection de deux Bi n'est pas disjointe et c'est pareil pour Ai'= X\Ai alors que c'est une propriété de la partition.

2) Désolé si je me suis mal exprimé. Oui c'est ta deuxième proposition. Voici ce que le texte dit : " Considérer la fonction u(x)=max (x(1-x), -x(1+x)). Notons v la mesure image de (mesure de Lebesgue) par la fonction u. Calculer v(]a,b]) pour tout a<b.
Soit f une fonction borélienne non négative. Démontrer que

I( f(y)v(dy))= I(f(u(x));)(dx)) (I c'est l'intégrale sur R). " Dans mon cours j'ai que la mesure image m de f par z s'écrit m(e)= f(z^(-1)[e]), c'est pour cela que je t'ai parlé de calculer la réciproque de u...

[Ben314]

Pour le 1), je comprend pas du tout "quoi c'est" que tu as essayé.
Si n=3 on a 3 ensembles (quelconques)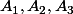 et ce que je te suggère de prendre, c'est








C'est clairement une partition de X (fait un dessin...) et on a




Et concernant le 2), il serait peut-être temps de comprendre que, lorsque E est une partie (et pas un élément) de l'ensemble d'arrivée de la fonction z, la notation z^-1(E) désigne l'ensemble des antécédents de E par z et que la notation en question ne sous entend absolument pas que la fonction z est bijective (i.e. il n'y a pas de "fonction réciproque" z^-1)
Rappel (piqûre...) si f:R->R;x->x² (pas du tout bijective !!!) alors f^-1(]-1,4])=[-2,2]

[Alpha77]

D'accord. Merci pour ton aide