Calcul d'aire sur excel

[dotty]

Bonjour à tous

je suis nouvelle sur le forum et pas très douée en math...

je fais appel à vous pour votre aide si précieuse.

Je cherche a calculer l'aire d'un quadrilatère convexe sur Excel. J'ai les coordonnées X et Y de 4 points
seulement j' ai utilisé la formule suivante :

J'ai fais :

(Xa*Yb)-(Ya*Xb) pour le premier point

puis pour le deuxième j'ai fais la même chose mais en descendant d'une ligne c'est à dire :
(Xb*Yc) - (Yb*Xc)
en gros je croise les coordonnées des points A,B,C,D ...

Ensuite j'utilise la formule Absolu en incluant la somme de tout les résultats que je divise par 2

J'aurai voulu savoir si ce que je fais est juste car j'ai des doutes en essayant sur papier je n'ai pas le même résultat...

n'hesite pas à me poser des questions si ce que je raconte n'est pas très clair :lol3:

Merci d'avance pour vos réponses ^^

[Dlzlogic]

Bonjour,
Excel est un outil de calcul.
Où avez-vous trouvé cette formule ?
L'avez-vous essayée à la main ?
Pourquoi cherchez-vous à calculer l'aire d'un polygone ?
Avez-vous pensé au dernier côté ?
Imaginez que les X soient de l'ordre de 1 million et les Y de l'ordre de 8 millions, que pensez- vous de la qualité du résultat ?
Ca fait 5 questions, ça fait beaucoup pour un samedi soir. :zen:

[chan79]

Bonjour à tous

je suis nouvelle sur le forum et pas très douée en math...

je fais appel à vous pour votre aide si précieuse.

Je cherche a calculer l'aire d'un quadrilatère convexe sur Excel. J'ai les coordonnées X et Y de 4 points
seulement j' ai utilisé la formule suivante :

J'ai fais :

(Xa*Yb)-(Ya*Xb) pour le premier point

puis pour le deuxième j'ai fais la même chose mais en descendant d'une ligne c'est à dire :
(Xb*Yc) - (Yb*Xc)
en gros je croise les coordonnées des points A,B,C,D ...

Ensuite j'utilise la formule Absolu en incluant la somme de tout les résultats que je divise par 2

J'aurai voulu savoir si ce que je fais est juste car j'ai des doutes en essayant sur papier je n'ai pas le même résultat...

n'hesite pas à me poser des questions si ce que je raconte n'est pas très clair :lol3:

Merci d'avance pour vos réponses ^^

Salut

Je diviserais simplement la norme du produit vectoriel de et par 2.



Uploaded with ImageShack.us

[dotty]

Bonjour,
Excel est un outil de calcul.
Où avez-vous trouvé cette formule ?
L'avez-vous essayée à la main ?
Pourquoi cherchez-vous à calculer l'aire d'un polygone ?
Avez-vous pensé au dernier côté ?
Imaginez que les X soient de l'ordre de 1 million et les Y de l'ordre de 8 millions, que pensez- vous de la qualité du résultat ?
Ca fait 5 questions, ça fait beaucoup pour un samedi soir. :zen:

Bonsoir et merci pour vôtre intérêt porté à ma question

- alors en fait cette formule je l'ai trouvé sur un forum à cette page : (Dans le fichier excel donné)
http://www.excel-downloads.com/forum/164156-calcule-aire-graphique-radar.html

- A la main j'ai divisé mon polygone en deux triangle puis tracé la hauteur pour calculé bxh / 2 pour les deux triangles. Enfin j'ai additionné mes résultats. Est ce faux ?

- je cherche à calculer cet aire dans le but d'estimer un volume je m'explique je travaille sur de l'érosion du à un ruissellement et je cherche à calculer le volume de sédiment qui s'est retiré.
j'ai pour cela réalisé 44 profils en travers le long de ce cours d'eau donc je comptais trouver l'aire de mon profil qui forme un polygone puis de le multiplier par une longueur a savoir 25 mètres d'écart entre tout mes profils. J'aurai ensuite additionner tout ça pour trouver le volume total ...

- Pour le dernier côté : dans l'exemple donné dans le forum ou j'ai pris cette formule le dernier points est calculé avec les coordonnées du premier points. C'est aussi ce que j'ai fait.

- A vrai dire je n'ai pas pensé au 8 millions ...

:marteau:

[dotty]

Salut

Je diviserais simplement la norme du produit vectoriel de et par 2.



Uploaded with ImageShack.us

Merci beaucoup pour ta réponse
je ne comprend pas beaucoup ta formule
en écriture scientifique ça donnerai quoi du coup ?

[Dlzlogic]

Bonsoir,
Je connais bien les méthodes de calcul de volumes par profils.
Il y a une autre méthode de calcul de volume, par surfaces horizontale, et dans votre cas de sédiments elle ma parait préférable.
Comme apparemment il ne s'agit pas d'un exercice scolaire, il me parait préférable de prendre le problème dès le départ. Ceci justifie mes 5 questions.
La méthode que vous employez est la méthode générale de calcul d'aire de polygone connus par les coordonnées des sommets (mais j'ai pas vérifié la formule elle-même ; de mémoire c'est 1/2 somme((xa+xb)*(ya-yb)) ) .Mais on verra ça demain.
Je vous ai parlé de coordonnées très grandes, parce que ce sont des valeurs habituelles en projection Lambert.

Donc, donnez-moi plus de détails sur les éléments dont vous disposer, leur forme etc. et je vous dirai de quelle façon je vois les choses. :dodo:

[dotty]

Bonsoir,

Alors sur le terrain j'ai relevés pour chaque profils :
- la largeur plein bord
- la largeur de fond de rivière
- la hauteur rive gauche
- La hauteur rive droite
c'est ce qui forme mes 4 points sur le polygone

Est ce, sur une longueur de 1km12 ce qui représente 44 profils.

Mais pour que ce soit le plus ressemblant possible à la réalité, j'ai réalisé ce que j'ai appelé des profils moyens en faisant la moyenne de deux profils qui se suivent ( peut être aurai-je dû plutôt utiliser la médiane ?) ce qui me fais au final 43 profils et non plus 44 ... et c'est à partir des profils moyens que je souhaite calculer le volume.

[Dlzlogic]

Bonjour,
Donc, vous avez relevé vous même, et sur le terrain, 4 points par profil, de la situation actuelle. Ce qui sous-entend que vous allez faire la même opération, dans un certain temps, pour constater et chiffrer la différence.
Je suppose que vous avez repéré vos profils.

Le fait de prendre les profils moyens ne change rien au résultat final, si on ne se trompe pas sur la distance d'application à prendre en compte au début et à la fin.

Donc, utilisez la formule 1/2 Somme((xa+xb) * (ya-yb)).
Pour la démonstration : l'aire d'un polygone est la somme de tous les trapèzes rectangles successifs.
Il est d'usage de considérer une aire comme essentiellement positive. Donc, on prend la valeur absolue du résultat.
Personnellement, mais il faut pas le répéter, le signe de l'aire d'un polygone me permet de déterminer le sens de rotation.

[dotty]

Bonjour,
Donc, vous avez relevé vous même, et sur le terrain, 4 points par profil, de la situation actuelle. Ce qui sous-entend que vous allez faire la même opération, dans un certain temps, pour constater et chiffrer la différence.
Je suppose que vous avez repéré vos profils.

Le fait de prendre les profils moyens ne change rien au résultat final, si on ne se trompe pas sur la distance d'application à prendre en compte au début et à la fin.

Donc, utilisez la formule 1/2 Somme((xa+xb) * (ya-yb)).
Pour la démonstration : l'aire d'un polygone est la somme de tous les trapèzes rectangles successifs.
Il est d'usage de considérer une aire comme essentiellement positive. Donc, on prend la valeur absolue du résultat.
Personnellement, mais il faut pas le répéter, le signe de l'aire d'un polygone me permet de déterminer le sens de rotation.

Bonjour,
Je suis désolé de ne pas avoir répondu. je viens de déménager et internet ne m'est revenu que depuis hier !

Tout d'abord, merci Dlzogic pour ton aide si précieuse ! cela dit avec cette formule je trouve des fois des chiffres exorbitant comme 33m2 pour l'un de mes profils qui a pour mesure AB= 104cm BC= 700cm CD= 121cm et AD= 760cm...
alors je ne comprends pas et je suis plus que perdu ...

[Dlzlogic]

Bonjour,
Envoyez-moi vos données, je crois que c'est le plus simple.
Mais, une question me tracasse : dans quel contexte faites-vous cela ? bien-sûr, sans aucune indiscrétion de ma part.
Dans votre exemple, on doit pas être loin de S= 1.12*7.30 = 8.2
Est-ce que par exemple, vous n'auriez pas oublié de diviser par 4 ?

[leon1789]

Je cherche a calculer l'aire d'un quadrilatère convexe sur Excel. (...)
- A la main j'ai divisé mon polygone en deux triangle puis tracé la hauteur pour calculé bxh / 2 pour les deux triangles. Enfin j'ai additionné mes résultats. Est ce faux ?

Il me semble que personne n'a répondu à cette question, pourtant simple.
La réponse est : ce n'est pas faux (c'est une méthode standard : on partage le polygone en triangles et on additionne les aires des triangles, chaque aire étant calculée par la formule : base * hauteur /2 ).

[Dlzlogic]

Il me semble que personne n'a répondu à cette question, pourtant simple.
La réponse est : ce n'est pas faux (c'est une méthode standard : on partage le polygone en triangles et on additionne les aires des triangles, chaque aire étant calculée par la formule : base * hauteur /2 ).

Les utilisateurs de cette formule doivent être assez rares.
Je pense à plusieurs méthodes de calcul d'aire, en plus de celle que j'ai indiquée : le planimètre, l'intégrateur à roulettes pour mesurer l'aire des peaux, la pesée après une découpe, plus une petite extension : calculs de volumes par pesée géométrique etc.

[leon1789]

Les utilisateurs de cette formule doivent être assez rares.

Oui, il existe d'autres formules pour calculer l'aire d'un triangle (quand on dispose de renseignements sur le triangle autre que la hauteur ou la base), mais apparemment celle-ci fonctionne dans le cas présent (puisque c'est dotty qui l'utilise).

Je pense à plusieurs méthodes de calcul d'aire, en plus de celle que j'ai indiquée : le planimètre, l'intégrateur à roulettes pour mesurer l'aire des peaux, la pesée après une découpe, plus une petite extension : calculs de volumes par pesée géométrique etc.

Je ne pense pas que cela soit utile de noyer le lecteur dans un océan de méthodes s'il ne les connaît pas. Il s'agit surtout de répondre de manière simple aux questions qui sont posées.

[deltab]

Bonjour.

Pour ceux qui veulent savoir comment Dotty calcules les aires

La méthode de calcul d'aire qu'utilise Dotty provient de la formule de Green-Riemann
appliquée au calcul d'aire: .
Ici, au lieu d'utiliser l'intégrale double on utilise l'intégrale curviligne pour le calcul d'aire.
Pour un triangle ABC orienté dans le sens trigonométrique, (on peut supposer que l'ordre
A-> B-> C-> A donne le sens trigonométrique quitte à renommer les sommets si nécessaire).
On aura alors


Le calcul d'aire est donc ramené au calcul de l'intégrale curviligne sur des segments de droites.

On peut généraliser la formule pour un quadrilatère convexe et plus généralement à un
polygone convexe en les décomposant en triangles. Les intégrales sur les côtés ajoutés
lors de la décomposition en triangles s'éliminent car on retrouve dans la somme finale
2 fois les intégrales sur ces côtes mais calculées dans deux sens différents.

Pour calculer l'intégral curviligne, , je ne vais pas trouver
l'équation de la droite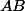 , mais calculer l'intégrale sur une droite ,
entre 2 points et de cette droite pris dans cet ordre. Si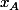
et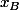 désignent les abscisses des points et , leurs
ordonnées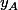 et 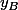vérifient alors .
On aura alors:



.

Finalement, l'intégrale s'exprime uniquement en fonction des coordonnées des 2 points A et B.

[Dlzlogic]

Bonsoir,
Si j'ai bien compris, vous calculez l'aire d'un quadrilatère à partir de 2 points, ou plutôt qui vous dites que Dotty calcule une aire à partir de 2 points ?
Je pense qu'il faudrait être un peu plus explicite concernant votre démonstration.

[deltab]

Bonjour.

@Dizlogic

Finalement, l'intégrale s'exprime uniquement en fonction des coordonnées des 2 points A et B.

Cette remarque ne concernait que l'intégrale curviligne sur le segment AB.

Pour l'aire d'un triangle ABC avec l'hypothèse que le sens A-> B-> C-> A donnait le sens trigonométrque, j'avais écrit:



Si on utilise la formule trouvée on aura alors
.

Pour un quadriltére convexe ABCD,on aura:

.

Pour un polygone convexe de sommets , , on aura:

[Dlzlogic]

Bonjour,
Je n'ai toujours pas compris le but de votre intervention.
Soit il s'agit de démontrer par des méthodes compliquées que les calculs simples et que l'on fait couramment sont justifiés, mais ça on le savait déjà, soit vous cherchez à prouver quelque-chose, et pour que je comprenne, une série de formules ne m'apporte rien, il faudrait un peu de texte, du genre "Soit une certain nombre ... mesuré de telle façon, cf.hypothèse ... ; on cherche à calculer ... donc je propose cette méthode ... en conclusion, la valeur cherchée est ..."
Là vous redémontrer la formule de calcul de l'aire d'une zone, qui se démontre aussi très facilement en géométrie, puisque c'est une application du produit vectoriel.