Branchement régulier et fonction analytique
14 messages
- Page 1 sur 1
Branchement régulier et fonction analytique
Soit ϕ (z) la branche régulière de la fonction analytique \ sqrt {\ frac {1 + z} {1-z}} dans le domaine C ∖ [- 1,1] fixé par la condition ϕ (0 + i0) = limε → 0 ϕ (iε) = 1.Dans mon cas, je veux trouver ϕ (−i), sincèrement je ne peux pas dire ce que j'ai essayé car je ne sais pas quoi faire pour commencer.
Je sais que la réponse est : -\sqrt{i} ou sqrt{i} mais je ne sais pas le prouver.
Je sais que la réponse est : -\sqrt{i} ou sqrt{i} mais je ne sais pas le prouver.
Re: Branchement régulier et fonction analytique
Bonjour,
Tu n'as pas dû recopier correctement la condition qui fixe la détermination. Tu as sans doute oublié un truc du genre " tend vers 0 par valeurs positives".
tend vers 0 par valeurs positives".
Tu n'as pas dû recopier correctement la condition qui fixe la détermination. Tu as sans doute oublié un truc du genre "
Re: Branchement régulier et fonction analytique
GaBuZoMeu a écrit:Bonjour,
Tu n'as pas dû recopier correctement la condition qui fixe la détermination. Tu as sans doute oublié un truc du genre "tend vers 0 par valeurs positives".
Ce n'est pas précisé dans mon énoncé mais cela me parait logique, juste.
Re: Branchement régulier et fonction analytique
Si la détermination a limite 1 quand on approche 0 par dessus, quelle est la limite quand on approche 0 par dessous ?
Re: Branchement régulier et fonction analytique
GaBuZoMeu a écrit:Si la détermination a limite 1 quand on approche 0 par dessus, quelle est la limite quand on approche 0 par dessous ?
Je ne sais pas mon prof nous a juste donner ça, donc si vous avez un suggestion en supposant que votre hypothèse est juste je demanderais à mon prof quand je le reverrai.
Re: Branchement régulier et fonction analytique
La question que je t'ai posée ne dépend pas de l'énoncé. Aussi je te demande d'y réfléchir.
Suggestion : partant d'un poil au dessus de 0, tu vas vers la gauche, fais le tour de -1 et reviens vers la droite un poil en dessous de 0. Tu peux réfléchir séparément à ce qui se passe pour la détermination de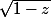 et celle de
et celle de 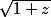 le long de ce chemin.
le long de ce chemin.
Suggestion : partant d'un poil au dessus de 0, tu vas vers la gauche, fais le tour de -1 et reviens vers la droite un poil en dessous de 0. Tu peux réfléchir séparément à ce qui se passe pour la détermination de
Re: Branchement régulier et fonction analytique
En réfléchissant séparément, j'en déduit que les arguments de \sqrt{1+z} et sqrt{1-z} sont les mêmes et donc que l'argument de \sqrt{1+z} /sqrt{1-z} est 0. Maintenant on veut déterminer le module de cette branche ?
Re: Branchement régulier et fonction analytique
Non, ce n'est pas correct. As-tu bien suivi ma suggestion ?
Que se passe-t-il pour l'argument de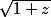 quand on suit le chemin que j'ai indiqué ?
quand on suit le chemin que j'ai indiqué ?
Que se passe-t-il pour l'argument de
Re: Branchement régulier et fonction analytique
Ben non. On part de z=0 (un peu au-dessus) et on revient à z=0 (un peu en-dessous), donc 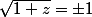 avec argument 0 ou
avec argument 0 ou  .
.
Re: Branchement régulier et fonction analytique
D'accord mais si on fait la même chose pour \srqt{1-z} l'argument vaut aussi 0 ou \pi
Re: Branchement régulier et fonction analytique
Je reformule la question, puisque tu sembles ne pas voir exactement où on va.
As-tu bien compris le chemin que je veux te faire suivre pour aller de 0 (un peu au-dessus) à 0 (un peu en-dessous) en tournant autour de - 1 ?
Si au début du chemin on est avec la détermination de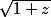 égale à 1 pour z=0 (donc d'argument 0), avec quelle détermination est-on à la fin du chemin ?
égale à 1 pour z=0 (donc d'argument 0), avec quelle détermination est-on à la fin du chemin ?
Même question pour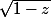 .
.
Ta réponse de "de \pi/2 à -\pi/2" ne va pas, bien sûr, puisqu'on part dans les deux cas avec un argument nul. Je voudrais une réponse correcte.
As-tu bien compris le chemin que je veux te faire suivre pour aller de 0 (un peu au-dessus) à 0 (un peu en-dessous) en tournant autour de - 1 ?
Si au début du chemin on est avec la détermination de
Même question pour
Ta réponse de "de \pi/2 à -\pi/2" ne va pas, bien sûr, puisqu'on part dans les deux cas avec un argument nul. Je voudrais une réponse correcte.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
