Hello à tous,
Utilisez l'axiome d'Archimède pour démontrer que si a ∈ IR tel que : 0 <= a <= 1/n pour tout n>= 1, alors a = 0
Qu’est-ce que l’aciome d’Archimède ? Comment l’utiliser pour cette question ?
Axiome d'Archimède et convergence
5 messages
- Page 1 sur 1
Re: Axiome d'Archimède et convergence
Je ne connaissais pas la dénomination "axiome d'archimède", mais la propriété " est un corps archimédien", c'est-à-dire, pour tout réels strictement positifs
est un corps archimédien", c'est-à-dire, pour tout réels strictement positifs  et
et  , il existe un entier naturel
, il existe un entier naturel  tel que
tel que  .
.
On peut alors utiliser cela en raisonnant par l'absurde, avec et
et 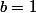
On peut alors utiliser cela en raisonnant par l'absurde, avec
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Axiome d'Archimède et convergence
Tu raisonnes pas l'absurde en supposant qu'un tel a existe et qu'il est strictement positif. C'est à dire que pour tout entier non nul n, 0<a<=1/n (*)
Or, par la propriété d'Archimède, il existe un entier naturel p tel que a*p>1
Mais alors, comme a>0, on obtient a>1/p : ce qui contredit (*) : c'est absurde
Conclusion : un tel a est forcément égal à 0.
Or, par la propriété d'Archimède, il existe un entier naturel p tel que a*p>1
Mais alors, comme a>0, on obtient a>1/p : ce qui contredit (*) : c'est absurde
Conclusion : un tel a est forcément égal à 0.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
