Avez vous trouvé?
16 messages
- Page 1 sur 1
Avez vous trouvé?
Bonjour,
Je résume pour faciliter
Voici l'algorithme sortant de l'équation P=NP
1=P+N devient,
P+1=1
N+1=1
P=(N+1)P
1=N+1
P=NP+P
Bien cordialement
Merci d'avance
Autrement
NP=0 Ce qui donne:
N=0 ou P=0
Ce qui donne
P=0
Vous avez montré votre niveau pour la première fois. On sait maintenant. On sait que vous ne comprenez pas tout en mathématiques.
P+1=1 veut dire P=0 ou
N+1=1 veut dire N=0
Enfin
P=(N+1)P veut dire P=0
Je résume pour faciliter
Voici l'algorithme sortant de l'équation P=NP
1=P+N devient,
P+1=1
N+1=1
P=(N+1)P
1=N+1
P=NP+P
Bien cordialement
Merci d'avance
Autrement
NP=0 Ce qui donne:
N=0 ou P=0
Ce qui donne
P=0
Vous avez montré votre niveau pour la première fois. On sait maintenant. On sait que vous ne comprenez pas tout en mathématiques.
P+1=1 veut dire P=0 ou
N+1=1 veut dire N=0
Enfin
P=(N+1)P veut dire P=0
Re: Avez vous trouvé?
Si tu ne comprends pas que j'ai résolu le problème P=NP c'est que tu connais rien en mathématiques.
P=NP équivaut à P=0 et NP=0
P=NP équivaut à P=0 et NP=0
Re: Avez vous trouvé?
Ce que tu écris n'a aucun rapport avec le problème P=NP.
En plus, tu oublies une flopée de solution de l'équation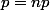 :
:  ,
,  quelconque.
quelconque. 
En plus, tu oublies une flopée de solution de l'équation

Re: Avez vous trouvé?
Tu parles sans rien connaître en mathématiques. Puisque N=1 est valable pour P quelconque car P=NP+P où P=0
Re: Avez vous trouvé?
Décidément on rigole bien.
Comment se fait-il que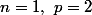 est solution de
est solution de 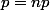 , mais pas de
, mais pas de 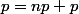 ?
?
Comment se fait-il que
Re: Avez vous trouvé?
Tous les solutions vérifient la même chose P=NP. Il y'a pas une autre vérification.
Re: Avez vous trouvé?
Tu ne réponds pas à ma question. Je vais la poser autrement : comment fais-tu pour déduire 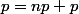 de
de 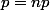 ?
?
Re: Avez vous trouvé?
Si vous ne comprenez pas ce qui est fait ici, qu'est-ce que vous connaissez en mathématiques ? Rien. Je viens de résoudre le problème P=NP et tu reviens me direz comment déduis tu P=NP+P de P=NP. Ça montre que vous ne comprenez pas.
Re: Avez vous trouvé?
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Avez vous trouvé?
vam a écrit:Çà doit être à la mode
effectivement car on en parle ici aussi https://forums.futura-sciences.com/mathematiques-superieur/929474-p-np-pire-demonstation-de-lhistoire.html
Re: Avez vous trouvé?
La rigolade continue !
Puisque tu as résolu P=NP, dépêche-toi de le publier pour gagner le million de $ promis par le Clay Mathematical Institute.
Mais je crains que tu sois déçu, car tu n'as rien compris à l'énoncé du problème P=NP :
https://claymath.org/millennium-problems/p-vs-np-problem
Et pire, tu n'arrives pas à traiter correctement l'équation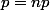 (ce qui n'a rien à voir avec le problème P=NP).
(ce qui n'a rien à voir avec le problème P=NP).
PS. Au moins, dans les autres loufoqueries au sujet de P=NP, on a une vague idée de quoi il retourne. Ce n'est absolument pas le cas ici.
Puisque tu as résolu P=NP, dépêche-toi de le publier pour gagner le million de $ promis par le Clay Mathematical Institute.
Mais je crains que tu sois déçu, car tu n'as rien compris à l'énoncé du problème P=NP :
https://claymath.org/millennium-problems/p-vs-np-problem
Et pire, tu n'arrives pas à traiter correctement l'équation
PS. Au moins, dans les autres loufoqueries au sujet de P=NP, on a une vague idée de quoi il retourne. Ce n'est absolument pas le cas ici.
Re: Avez vous trouvé?
P=NP c'est P=0 ou NP=0
1) Calculons NP=0
P+1=1
N+1=1
2) Calculons P=0 aussi
P=(N+1)P
La preuve montrant P=(N+1)P
P=NP+P quand P=NP alors P=0
C'est lapeine d'écrire N+1=1 puisque P=(N+1)P est aussi égale à N+1=1 et P=NP+P
1) Calculons NP=0
P+1=1
N+1=1
2) Calculons P=0 aussi
P=(N+1)P
La preuve montrant P=(N+1)P
P=NP+P quand P=NP alors P=0
C'est lapeine d'écrire N+1=1 puisque P=(N+1)P est aussi égale à N+1=1 et P=NP+P
Re: Avez vous trouvé?
Le comique de répétition a ses limites !
1°) Ça n'a rien à voir avec le problème P=NP
2°) Il est faux que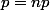 entraîne
entraîne 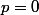 , puisque
, puisque 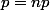 est vérifié pour
est vérifié pour 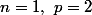 .
.
P=NP c'est P=0 ou NP=0
1°) Ça n'a rien à voir avec le problème P=NP
2°) Il est faux que
Re: Avez vous trouvé?
Je vais pas continuer à parler avec toi, tu es un trolls et pire que ça. Moi je m'adresse aux intelligents pas aux trolls comme toi
Re: Avez vous trouvé?
Bonjour Hamma,
non seulement tu ne fait aucun effort de compréhension, mais en plus tu insultes tes interlocuteurs.
Au revoir.
P.S: ce qu'à dis GBZM est parfaitement exact
1) tes dires n'ont rien à voir (mais vraiment rien) avec le célèbre problème P=NP où P et NP correspondent à des classes de complexités de problèmes (et certainement pas des nombres)
2) l'équation a = a*b que tu sembles vouloir résoudre admet bien d'autres solutions (niveau 3ème a peu près):
a-a*b=0
a(1-b)=0
a=0 OU b=1
non seulement tu ne fait aucun effort de compréhension, mais en plus tu insultes tes interlocuteurs.
Au revoir.
P.S: ce qu'à dis GBZM est parfaitement exact
1) tes dires n'ont rien à voir (mais vraiment rien) avec le célèbre problème P=NP où P et NP correspondent à des classes de complexités de problèmes (et certainement pas des nombres)
2) l'équation a = a*b que tu sembles vouloir résoudre admet bien d'autres solutions (niveau 3ème a peu près):
a-a*b=0
a(1-b)=0
a=0 OU b=1
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
