Arithmétique et divisibilité

[guillaume100]

Bonjour à tous,

Soient a et b des nombres premiers entre eux. Considérons leur produit a*b. Les diviseurs de a*b sont alors les diviseurs de a et les diviseurs de b.

Dans un concours, ils affirment que c'est vrai.
Comment le montrer ? J'ai essayé d'utiliser les valuations mais je n'ai pas réussi !

Merci bien

[mathelot]

bonsoir,
ça me parait faux
a*b est un diviseur de a*b sans diviser nécessairement a ou b.

[FLBP]

Salut
N'était-ce pas ça plutôt ?
https://fr.wikipedia.org/wiki/Lemme_d%27Euclide

[Ben314]

Salut,
C'est évidement on ne peut plus clairement archi faux ton truc : les diviseurs de 2x2, c'est évidement pas les mêmes que les diviseurs de 2 !!!!!

Par contre, le truc systématiquement vrai quelque soient et , c'est que les diviseurs du produit 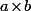sont tous de la forme 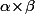où divise et divise et que réciproquement, tout nombre de cette forme divise le produit .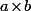
Et si de plus, et sont premiers entre eux, alors tout diviseur (positif) du produit 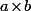s'écrit de façon unique sous la forme 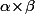où divise et divise .
Et ça fourni une bijection de l'ensemble sur l'ensemble qui permet par exemple de montrer que le nombre de diviseurs de 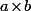c'est le nombre de diviseurs de multiplié par le nombre de diviseurs de .

[guillaume100]

Salut,

Merci pour vos réponses ! Je m'étais trompé dans le sujet, c'est bien les diviseurs de a*b s'écrivent en fonction des diviseurs de a ou b, et c'est une bijection si a et b sont premiers entre eux (merci Ben314). Du coup je l'ai pas démontré avec le lemme d'Euclide ni celui de Gauss mais je l'ai montré en décomposant a et b en facteurs premiers.

Un diviseur de a*b s'écrit alors facilement en un diviseur de a multiplié par un diviseur de b.

Pour l'unicité cela se montre aussi avec la décomposition en facteurs premiers puisque a et b sont premiers entre eux et ont pas de facteurs communs.

Merci bien !