Arccos

[alex1236]

bonjour, j'ai un petit souci avec un exercice qui consiste à simplifier l'expression suivante :

f(x)=arccos(cos(3x)) où x appartient à [(-pi/2);(pi/2)]

or arcos est défini sur [-1;1] et cos(Y) quelque soit Y appartient toujours à [-1;1] donc l'expression devrait toujours être égale à f(x)=3x .

Je ne comprends donc pas pourquoi il faut décomposer l'exercice en plusieurs intervalles ...????

Merci d'avance pour vos réponses .

[Ben314]

NON : la fonction cos N'EST PAS une bijection de R->[-1,1] donc la fonction ArcCos n'est pas la bijection réciproque de cette fonction mais SEULEMENT d'une restriction de cette fonction.
Cela provoque des résultat qui, au premier abord, peuvent paraitre surprenant : pour tout x réel on PEUT CALCULER ArcCos(cos(x)), mais le résultat n'est x que si x est dans le 'bon intervalle'...

C'est exactement comme la fonction racine carré qui N'EST PAS la bijection réciproque de x->x^2 sur R.
Cela provoque que racine(x^2) n'est pas tout le temps égal à x...

[alex1236]

alors je te crois totalement mais j'ai l'impression d'avoir toujours appris que cos était compris entre -1 et 1 . Et depuis taleur je suis entrai de chercher un x qui contredirait ça et je n'en trouve aucun... :triste:

[Ben314]

Le problème n'est pas là : cos(x) est bien toujours entre -1 et 1.
Le problème est que la fonction ArCos est la bijection réciproque de la fonction Cos vue comme fonction de [0,pi] dans [-1,1].

Cela signifie que
0) Pour tout y dans [-1,1], Arcos(y) est dans [0,pi].
1) Pour tout x dans [0,pi], ArcCos(cos(x))=x
2) Pour tout y dans [-1,1], cos(ArcCos(y))=y

Pour la formule du 2), il n'y a rien à rajouter mais pour celle du 1) cela pose un problème car, lorsque x n'est pas dans [0,pi], on peut tout de même calculer ArcCos(cos(x)) mais le résultat n'est surement pas égal à x car l'ArcCos de n'importe quoi est toujours dans [0,pi].

Essaye (à l'aide d'un cercle trigo) de voir combien vaut ArcCos(-pi/4), ArcCos(-pi/2), ArcCos(5pi/4)...

Je te (re)dit : cela ressemble au "piége" pour lycéens : racine(x^2) n'est pas toujours égal à x. Ce n'est vrai que si x est positif...

[wserdx]

Hum, ça ne change rien aux propos de Ben, mais il y a eu récemment une question sur ce forum concernant arcos, dont la réponse m'a surpris mais juste
La fonction "arcos" est
impaire?
paire?
positive?
négative?

La réponse est : positive!
eh oui, elle est définie à valeurs dans

!

[Ben314]

Putain, c'est ma deuxième connerie de la journée : je modifie immédiatement !!!
P.S. pour ceux qui arrivent aprés modification :
J'avais pris l'intervalle [-pi/2,pi/2] comme domaine fondamental pour le cos !!! la honte

[Ourfalli]

Bonsoir,
Une petite contribution:
Nous n'avons pas le droit d'écrire ou plutôt avant de définir la composée de ces deux fonctions :


La composée est possible:


Si on prend les restrictions :




Alors, on a la restriction :



à vérifier.

[busard_des_roseaux]

bonjour,

la composée de fonctions arccos ° cos() agit sur le réel
un peu comme un résidu.

cette composée renvoie comme image le réel
qui a même cosinus que mais qui est situé dans l'intervalle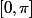

arccos(cos(x)) se lit : c'est l'arc de cercle dont le cosinus vaut cos(x)



cette composée est donc une fonction affine par morceaux.


soit le point M(cosx,sinx) du cercle trigo d'abscisse curviligne x
est situé sur le demi cercle supérieur (sinx>0), on se ramène au
bon intervalle par une translation d'un multiple entier de
alors pour un certain entier relatif k
soit M est situé en dessous de l'axe x'ox (sinx<0) et on effectue d'abord
une symétrie d'axe x'ox.
alors


Ourfalli:
on a cos(arccos(x))=x. surjectivité du cosinus=inversible à droite
défaut d'injectivité du cosinus= non
inversible à gauche.

[Ourfalli]

Oui, busard_des_roseaux :
Cos(Arccos(x)) : quel est le cosinus de l'angle dont le cosinus est x ? La réponse est contenue dans la question car cos est surjective.
Arccos(Cos(x)): quel est l'angle dont le cosinus est le cosinus de l'angle x? La réponse serait "lequel?" car cos n'est pas injective.

Donc, simplifier où n'est pas possible sans l'intervalle "d'arrivée" de la fonction f, et cet intervalle doit être choisi de telle manière qu'il fournisse une image unique de x (sinon f ne serait pas une fonction).

Donc la question revient à résoudre l'équation , puis choisir x en fonction de la définition de la fonction f.

J'aurais dû voir ça dès le départ...