Arc paramétré

[Thildoucantal15]

Bonjour,

Je dois faire l'étude de l'arc paramétré x(t)= sin(3t)
y(t) = (sin²(t))(2+sin(2t))
Seulement, je n'arrive pas à déterminer le signe de y'(t) sur l'intervalle (pi/2,pi)
y'(t)=2(sin²(2t)+sin(2t)-sin²(t))
Auriez vous des idées de méthodes?

Merci! :)

[mathelot]

or




sur , sin(t) est positive décroissante. Par composition
avec le carré,

est positive décroissante.




sur ,
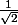
décroit de à

[Thildoucantal15]

or

cela permet d'accéder au signe de y(t) mais on a toujours le même problème pour le signe de y'(t), non?
(je n'ai pas encore tenté l'étude avec cette forme de y(t) mais j'essaye tout de suite)

[Thildoucantal15]

or




sur , sin(t) est positive décroissante. Par composition
avec le carré,

est positive décroissante.




sur , cos(t-\frac{\pi}{4})
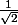
décroit de à

je n'avais pas vu la fin du message...
Merci beaucoup!!

[mathelot]

mais on a toujours le même problème pour le signe de y'(t), non?

oui, je cherche...

je n'avais pas vu la fin du message...
Merci beaucoup!!

il y a un intervalle sur lequel on ne peut toujours pas conclure.

[mathelot]

j'ai trouvé une méthode.









on pose comme variable x=tan(t)



après mise au dénominateur commun (avec x=tan(t))

[Thildoucantal15]

oui, je cherche...



il y a un intervalle sur lequel on ne peut toujours pas conclure.

oui c'est (3*pi/4, pi), c'est ça?

[mathelot]

oui c'est (3*pi/4, pi), c'est ça?

oui, c'est ça.

Je suis en train de tout passer en variable x=tan(t)
pour avoir à dériver une fraction rationnelle en x.

Comme on dérive par rapport à t, d'après le thm des fonctions
composées, il suffira de multiplier la dérivée ,relativement à x, par

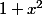
[Thildoucantal15]

j'ai trouvé une méthode.









on pose comme variable t=tan(x)



après mise au dénominateur commun

j'ai obtenu la même chose, mais j'ai un problème au niveau de la dérivée...
J'obtiens y'(t)= t(-12t^5+20t^4+16t^3+24t²+12t+4)/(t^4+2t²+1)²

On a toujours un problème pour en déterminer le signe...

[mathelot]

(avec x=tan(t))

j'en suis là....

[mathelot]

après mise au dénominateur commun (avec x=tan(t))

je dérive avec la dérivée logarithmique

(on calcule mentalement ln(|y|) que l'on dérive.)



d'après ma calculatrice,y' a le signe de

[Thildoucantal15]

je dérive avec la dérivée logarithmique

(on calcule mentalement ln(|y|) que l'on dérive.)



d'après ma calculatrice,y' a le signe de

Je ne connais pas du tout la dérivée logarithmique...

[mathelot]

Je ne connais pas du tout la dérivée logarithmique...

ici

.................................