Approximation de cos grâce à Taylor.

[Anonyme]

Bonsoir,

Je dois calculer avec "niveau de précision 10^-5" la valeur de cos(pi/20).

Je ne sais pas comment faire ceci. Je sais qu'il faut utiliser le développement limité de Taylor, seulement je ne sais pas quoi faire du "reste" et comment utiliser la condition de précision.

Si quelqu'un peut me donner un coup de main.. Je ne trouve pas vraiment d'exercices similaires qui pourrait me mettre sur la voix dans mes bouquins de cours.

Merci d'avance ! :lol3:

[mat2u]

En toute logique, tu dois poursuivre le développement de Taylor jusqu'à ce que le reste soit inférieur à .

[mathelot]

bonjour

posons


(E)

puis nous appliquons la méthode de Newton de calcul
d'une valeur approchée de la solution de (E1)

(E1)

[Anonyme]

Bonsoir,

Merci tous deux pour vos réponses,

@mathelot, je ne suis pas sûr de bien saisir, tu n'utilises pas du tout le développement limité de Taylor ? Je ne connais pas ta méthode, peux-tu expliquer un peu plus d'où ça vient ? Merci.

[Kikoo <3 Bieber]

Hello,

Mathelot utilise les polynômes de Tchebychev

[mathelot]

oui, ta valeur de cosinus est racine d'un polynome de Tchebyshev , le polynome on le construit à la main en appliquant cos(2x)=f(cosx), deux fois , et puis, une fois l'équation trouvée
, vérifiée par le , un peu de méthode de Newton

pour l'approcher.

tu peux coupler ça avec un calcul d'erreur sur l'approximation de racine de 5 (méthode de Héron)
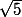, n'étant pas décimal , les calculs d'incertitudes pouvant ressembler à

[mathelot]

bonjour,
la méthode indiquée ne converge pas ici (même en divisant par 8).
Il faut dire que le polynome , plus généralement est très particulier,
si mes souvenirs sont exacts il a toutes ses racines dans un voisinage de [-1;1]

on va chercher autre chose.

[mathelot]

Bonjour,

la formule de Taylor-Maclaurin s'écrit

avec

et

la valeur exacte est


si tu dispose d'une calculatrice , tester avec

[Anonyme]

Re, :)

Ok, merci beaucoup pour le coup de main ! ;).

[Black Jack]

développement de Taylor de cos(x) :

cos(x) = 1 - x²/(2!) + x^4/(4!) - ... + (-1)^n x^(2n)/((2n)!) + ...

On peut montrer (critère de Leibniz) que pour x = Pi/20, la série ci dessus est convergente et que l'erreur faite en arrêtant la série à un certain terme est inférieure ou égale en valeur absolue à la valeur absolue du 1er terme négligé.

Il faut donc trouver la valeur min de n telle que (Pi/20)^(2n)/((2n)!) <= 10^-5 ... on trouve n = 3

On peut donc négliger le terme en n = 3 et donc se limiter à n = 2

et donc la valeur cherchée est : [1 - x²/(2!) + x^4/(4!)] avec x = Pi/20


1 - (Pi/20)²/(2!) + (Pi/20)^4/(4!)
= 1 - (Pi/20)²/2 + (Pi/20)^4/24
= 0,98768836 avec une erreur <= en valeur absolue à (Pi/20)^6/(6!) = 2,09.10^10^-8

--> cos(Pi/20) = 0,98769 à moins de 10^-5 près.

:zen:

[Kikoo <3 Bieber]

Salut Black Jack !

Justement, comment montres-tu que l'erreur commise est inférieure en valeur absolue à la valeur absolue du premier terme négligé ?

[Black Jack]

[quote="Kikoo u2 > u3 > ... et si lim(n--> +oo) un = 0, la série converge, sa somme est positive et n'est pas supérieure au 1er terme de la série.

Par extension immédiate de ce théorème, on a :
Si on a une série alternée : u1 - u2 + u3 - u4 + ... où u1 > u2 > u3 > ... et si lim(n--> +oo) un = 0, la série converge et l'erreur qu'on fait en négligeant les termes à partir d'un certain rang est inférieure en valeur absolue à la valeur absolue du premier terme négligé.

La démo est dans tout bon bouquin de math traitant des séries.

:zen:

[Kikoo <3 Bieber]

Ok merci Black Jack ! Je sais que tu n'es pas à même de me démontrer cela (car la démo ne vient pas de toi, par exemple), mais je me demandais si l'on voit ça en sup. Mon DM traite en partie de la convergence de séries alternées mais on est censés traiter ça en spé il me semble.

[Black Jack]

Ok merci Black Jack ! Je sais que tu n'es pas à même de me démontrer cela (car la démo ne vient pas de toi, par exemple), mais je me demandais si l'on voit ça en sup. Mon DM traite en partie de la convergence de séries alternées mais on est censés traiter ça en spé il me semble.

Je peux le démontrer, mais à quoi bon ?
La démo est dans mon bouquin de Math favori et cela me suffit.
L'important est de le connaître (pas la démo, le théorème) pour s'en servir quand c'est utile pour résoudre un problème concret.

Quant aux programmes actuels de Math dans les différents niveaux, je ne les connais pas.

:zen:

[Anonyme]

Merci bien Black Jack :).

(pour la physique, je n'ai pas encore répondu, mais je suis dessus ^^).

:lol3:

[mathelot]

bonjour,

en posant
et sont adjacentes, d'où