Application loi normale aux tests

par **Dante0** » 13 Déc 2013, 22:43

Bonsoir,

Dans le cadre d'un exercice sur les tests, on est amené à chercher :

avec

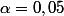
On a ensuite

, on trouve cette valeur parce qu'on cherche la probabilité 0,95 dans la table normale, mais pourquoi on cherche la probabilité de

?

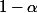
J'ai un problème avec ces schémas, je ne sais pas si vous voyez ce dont je parle, le schémas de la loi normale avec des aires grisées aux deux extrémités, représentant

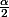
et les quantiles en bas...

Merci d'avance !

par **mrif** » 14 Déc 2013, 00:40

La table de la loi normale relie les nombres x et p définis par:
P(X [B] x) = 1-p ou P(X >= x) = 1-p car P(X = x) = 0

par **Dante0** » 14 Déc 2013, 09:15

mrif a écrit:La table de la loi normale relie les nombres x et p définis par:
P(X [B] x) = 1-p ou P(X >= x) = 1-p car P(X = x) = 0

Ok et si on avait eu

on aurait trouvé comment ? Puisque p = 0,05 n'est pas sur la table..

par **Ben314** » 14 Déc 2013, 11:04

Dante0 a écrit:Ok et si on avait eu on aurait trouvé comment ? Puisque p = 0,05 n'est pas sur la table..

Dans ce cas tu utilise la symétrie de la courbe qui te dit que p(Xa)=1-p(X<a) pour tout réel a.

par **Dante0** » 14 Déc 2013, 11:34

[quote="Ben314"]Dans ce cas tu utilise la symétrie de la courbe qui te dit que p(Xa)=1-p(X P(\frac{\bar{X_n}}{\sqrt{\frac{1}{n}}} 1-P(\frac{\bar{X_n}}{\sqrt{\frac{1}{n}}} < \frac{c}{\sqrt{\frac{1}{n}}}) = 0,95
[/TEX]
C'est cela ?

Ca s'applique uniquement à la loi normale ? Ou c'est également le cas pour la student ?

par **Ben314** » 14 Déc 2013, 11:48

La dernière équivalence, c'est plutôt

Sinon, ben ça s'applique à tout loi "symétrique", c'est à dire telle que le fonction de densité soit paire (

pour tout réel t) donc à la loi de Student.

par **Dante0** » 14 Déc 2013, 12:12

Ben314 a écrit:La dernière équivalence, c'est plutôt

Sinon, ben ça s'applique à tout loi "symétrique", c'est à dire telle que le fonction de densité soit paire ( pour tout réel t) donc à la loi de Student.

Donc on fini par tomber sur :

Le signe moins n'est pas génant ici ? On fait comment pour trouver la valeur de c ?
D'ailleurs c'est la valeur de c ou de X barre n qu'on cherche ? :mur:

par **Ben314** » 14 Déc 2013, 15:25

Ben non, le signe "moins" n'est absolument pas gênant : la loi normale prend des valeurs positives et des valeurs négatives et, comme p(X>0)=1/2, il est clair que le c tel que p(X>c)=0.95 va être négatif !
Après, la valeur de

(et sauf erreur, c'est bien elle que tu cherche), tu va la trouver à l'aide d'une table et tu en déduira la valeur de c.

par **Dante0** » 14 Déc 2013, 18:46

Ben314 a écrit:Ben non, le signe "moins" n'est absolument pas gênant : la loi normale prend des valeurs positives et des valeurs négatives et, comme p(X>0)=1/2, il est clair que le c tel que p(X>c)=0.95 va être négatif !
Après, la valeur de (et sauf erreur, c'est bien elle que tu cherche), tu va la trouver à l'aide d'une table et tu en déduira la valeur de c.

J'ai pas trop compris le lien ici.

par **Ben314** » 14 Déc 2013, 19:16

Dante0 a écrit:J'ai pas trop compris le lien ici.

Si cc contient l'ensemble des X tels que X>0 donc p(X>c)>p(x>0).
C'est le cas pour absolument n'importe quelle loi : la fonction de répartition est forcément croissante.

par **Dante0** » 14 Déc 2013, 19:42

Ok je m'enfonce un peu la ^^
Donc a partir de ca

je fais comment pour trouver la valeur de c ? Je regarde à p = 0,95 sur la table ?

par **Ben314** » 14 Déc 2013, 20:32

Oui, vu que

et que la table ne donne que les p(x<?).
Ensuite tu en déduira la valeur de c (qui va être franchement négative)

par **Dante0** » 14 Déc 2013, 21:12

Ok merci ! :)
Tu t'y connais en procédure de tests ? Le sujet que j'ai crée n'a pas beaucoup de succès. :triste:

Application loi normale aux tests

Application loi normale aux tests

Qui est en ligne