Angle plan; angle solide
4 messages
- Page 1 sur 1
angle plan; angle solide
Bonsoir pourrait-on me donner une définition assez compréhensible de l'angle plan et de l'angle solide.
théorie des angles
bjr,
il faut donner un aperçu de la théorie des angles
(voir par exemple Bourbaki) :
1) à l'école élémentaire, un angle (géométrique) est un secteur, une portion
de plan compris entre deux demi-droites
On peut les ajouter tant que la somme ne dépasse pas un angle
plein.
2) Après le Bac, on s'intéresse aux transformations du plan
vectoriel qui conservent le produit scalaire et l'orientation.
on montre que ces transformations forment un groupe
commutatif, pour la composition des applications
et que leur matrice, dans une base
orthonormée , sont de la forme:
)
avec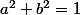
Ces transformations sont appelées rotations.
l'angle que font deux vecteurs unitaires et
et  est l'unique rotation r telle que
est l'unique rotation r telle que
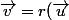)
l'angle plat correspond donc à la rotation r telle que
c'est l'angle que forment deux vecteurs opposés.
On définit la somme de deux angles comme la composée
des deux rotations coorespondantes.
Ensuite, la partie des maths qu'on appelle l'analyse complexe permet
d'associer surjectivement (fonction exponentielle complexe)
à un nombre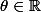 une rotation (donc un angle).
une rotation (donc un angle).
de manière :
 = R( \theta) o R(\theta '))
Le noyau de cette application est un sous-groupe discret de noté
noté  ,
,
Le cosinus étant alors la partie réelle du nombre complexe) ,
, ) de module 1, vecteur unitaire
de module 1, vecteur unitaire  d'affixe
d'affixe ) et aussi identifé à l'angle
et aussi identifé à l'angle
polaire) :
:
=\Re (f(\theta)) = \Re \left( \sum_{k=0}^{+\infty} \, \frac{{(i \theta)}^k}{k!} \right))
le nombre étant le plus petit zéro positif de la fonction cosinus. On retrouve ainsi le nombre
étant le plus petit zéro positif de la fonction cosinus. On retrouve ainsi le nombre  qui est aussi
qui est aussi
le coeff de proportionnalité entre le diamètre et la circonférence de tout cercle ainsi qu'entre l'aire et le carré du rayon.
Ceçi permet de mesurer les angles modulo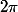 en
en
leur associant une famille de mesures, deux mesures quelconques
différant d'un multiple entier de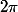 .
.
Ensuite, en géométrie affine, on réalise un angle de demi-droites affines
sécantes en un point O, comme l'angle que font leurs vecteurs directeurs.
La mesure d'un angle en unité radian, , géométriquement, est alors la longueur de l'arc de cercle de rayon 1, centré en O, sommet de l'angle.
, géométriquement, est alors la longueur de l'arc de cercle de rayon 1, centré en O, sommet de l'angle.
Pour les angles de droites, on doit identifier (cad, confondre)
quatre angles de deux demi-droites de même sommet.
On identifie alors les couples de vecteurs (u,v) (-u,-v) (u,-v) (-u,v)
et l'on mesure ces angles modulo .
.
Cordialement,
[Bourbaki vaut bien une majuscule.AD]
il faut donner un aperçu de la théorie des angles
(voir par exemple Bourbaki) :
1) à l'école élémentaire, un angle (géométrique) est un secteur, une portion
de plan compris entre deux demi-droites
On peut les ajouter tant que la somme ne dépasse pas un angle
plein.
2) Après le Bac, on s'intéresse aux transformations du plan
vectoriel qui conservent le produit scalaire et l'orientation.
on montre que ces transformations forment un groupe
commutatif, pour la composition des applications
et que leur matrice, dans une base
orthonormée , sont de la forme:
avec
Ces transformations sont appelées rotations.
l'angle que font deux vecteurs unitaires
l'angle plat correspond donc à la rotation r telle que
c'est l'angle que forment deux vecteurs opposés.
On définit la somme de deux angles comme la composée
des deux rotations coorespondantes.
Ensuite, la partie des maths qu'on appelle l'analyse complexe permet
d'associer surjectivement (fonction exponentielle complexe)
à un nombre
de manière :
Le noyau de cette application est un sous-groupe discret de
Le cosinus étant alors la partie réelle du nombre complexe
polaire
le nombre
le coeff de proportionnalité entre le diamètre et la circonférence de tout cercle ainsi qu'entre l'aire et le carré du rayon.
Ceçi permet de mesurer les angles modulo
leur associant une famille de mesures, deux mesures quelconques
différant d'un multiple entier de
Ensuite, en géométrie affine, on réalise un angle de demi-droites affines
sécantes en un point O, comme l'angle que font leurs vecteurs directeurs.
La mesure d'un angle en unité radian,
Pour les angles de droites, on doit identifier (cad, confondre)
quatre angles de deux demi-droites de même sommet.
On identifie alors les couples de vecteurs (u,v) (-u,-v) (u,-v) (-u,v)
et l'on mesure ces angles modulo
Cordialement,
[Bourbaki vaut bien une majuscule.AD]
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
