Bonjour
Cela fait plusieurs heures que je suis bloqué sur cette exercice
J'ai bien compris qu'il fallait trouver deux polynômes qui ne soit pas linéairement dépendant mais je n'y arrive pas dans le cas d'une intégrale .J'espère que vous pourrez m'aider.
Merci d'avance
voici le lien de l'exercice https://sercalwims.ig-edu.univ-paris13. ... indow=true
Algèbre linéaire base polynôme intégrale exercice sur wims
6 messages
- Page 1 sur 1
Re: algèbre linéaire base polynôme intégrale exercice sur wi
sinon je vous écris l'énoncé car je ne sais pas si j'ai le droit de mettre un lien donc le voici
Soit E l'espace vectoriel des polynômes d'une variable X et de degré inférieur à 2 et soit S le sous-espace vectoriel de E formé des polynômes P(X) tels que
∫−2−3 (intégrale de -3 à -2) P(x)dx=0 .
Trouver une base de S.
Première question: Trouver la dimension de S ça c'est bon j'ai mis 2
Deuxième question: Maintenant entrez la base avec 2 éléments P1 et P2
j'arrive a trouver un P1 mais je n'arrive pas à trouver un P2 qui soit linéairement indépendant de P1
Soit E l'espace vectoriel des polynômes d'une variable X et de degré inférieur à 2 et soit S le sous-espace vectoriel de E formé des polynômes P(X) tels que
∫−2−3 (intégrale de -3 à -2) P(x)dx=0 .
Trouver une base de S.
Première question: Trouver la dimension de S ça c'est bon j'ai mis 2
Deuxième question: Maintenant entrez la base avec 2 éléments P1 et P2
j'arrive a trouver un P1 mais je n'arrive pas à trouver un P2 qui soit linéairement indépendant de P1
Re: algèbre linéaire base polynôme intégrale exercice sur wi
Une ambiguïté dans l'énoncé : degré inférieur ou égal à 2 ou degré strictement plus petit que 2 ???
Mettons que c'est inférieur ou égal, auquel cas la réponse "dim(S)=2" est correcte.
Les éléments de S sont donc les polynômes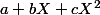 tels que
tels que \,dx=0) .
.
Comment procèdes-tu pour trouver une base de S ?
Mettons que c'est inférieur ou égal, auquel cas la réponse "dim(S)=2" est correcte.
Les éléments de S sont donc les polynômes
Comment procèdes-tu pour trouver une base de S ?
Re: algèbre linéaire base polynôme intégrale exercice sur wi
Merci pour votre réponse du coup j'ai trouvé le problème.
En fait il y'avait bien une ambiguité sur le inférieur à deux qui est bien inférieur ou égale à deux et du coup moi je croyais que c'était strictement inférieur à deux et je n'arrivait pas à trouver deux polynômes de degrés inférieurs à deux et à la fois base de S (donc non dépendants à mon avis c'était mathématiquement impossible mais bon...) .Ainsi en testant avec un polynôme de degrés un et trinôme du second degrés j'ai pu réussir l'exercice .
Et sur ma façon de procédé: j'essayais plusieurs solutions jusqu'à trouver la bonne réponse c'est surement pas la bonne méthode mais sur wims cela m'a sauvé la mise plus d'une fois .
Encore merci et j'avais une autre question qui est sur le même thème mais qui concerne des vecteurs et des espaces vectoriels est ce que je peux la poser sur ce post ou je dois en créé un autre ?
En fait il y'avait bien une ambiguité sur le inférieur à deux qui est bien inférieur ou égale à deux et du coup moi je croyais que c'était strictement inférieur à deux et je n'arrivait pas à trouver deux polynômes de degrés inférieurs à deux et à la fois base de S (donc non dépendants à mon avis c'était mathématiquement impossible mais bon...) .Ainsi en testant avec un polynôme de degrés un et trinôme du second degrés j'ai pu réussir l'exercice .
Et sur ma façon de procédé: j'essayais plusieurs solutions jusqu'à trouver la bonne réponse c'est surement pas la bonne méthode mais sur wims cela m'a sauvé la mise plus d'une fois .
Encore merci et j'avais une autre question qui est sur le même thème mais qui concerne des vecteurs et des espaces vectoriels est ce que je peux la poser sur ce post ou je dois en créé un autre ?
Re: algèbre linéaire base polynôme intégrale exercice sur wi
Un seul problème par fil, un un seul fil par problème.
Je ne suis pas sûr qu'essayer au hasard des réponses sur wims soit le meilleur moyen de comprendre.
Je ne suis pas sûr qu'essayer au hasard des réponses sur wims soit le meilleur moyen de comprendre.
Re: algèbre linéaire base polynôme intégrale exercice sur wi
ok merci pour l'histoire du fil des questions.
Par contre vous n'avez pas compris je ne mettais pas au hasard des réponses dans wims je cherchais la réponse sur papier en essayant plusieurs polynôme jusqu'à trouver le bon je sais que ce n'est pas très formel mathématiquement mais c'est une technique qui marche dans cette situation. Mais ne vous en faites pas j'ai compris l'objectif de l'exercice.
Encore merci
Par contre vous n'avez pas compris je ne mettais pas au hasard des réponses dans wims je cherchais la réponse sur papier en essayant plusieurs polynôme jusqu'à trouver le bon je sais que ce n'est pas très formel mathématiquement mais c'est une technique qui marche dans cette situation. Mais ne vous en faites pas j'ai compris l'objectif de l'exercice.
Encore merci
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
