139 résultats trouvés
Revenir à la recherche avancée
zygomatique a écrit:salut
h est définie sur ]0, 1[ et y > 0 donc il faut 0 < x/y < 1 ...
ensuite dérivée de fonctions composées ...
pour calculer les dérivées partielles seconde de f je passe par les dérivées partielles de h en utilisant la dérivée composé ?
- par Raphoul
- 19 Mar 2015, 19:46
-
- Forum: ✯✎ Supérieur
- Sujet: fonction plusieur variables
- Réponses: 7
- Vues: 661
Bonjour
je bloque sur une question d'un exercice
j'ai :

de classe

. On pose pour
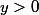
=h(\frac{x}{y}))
je dois déterminer

l'ensemble de définition de f
je ne sais pas comment faire
merci
- par Raphoul
- 19 Mar 2015, 17:22
-
- Forum: ✯✎ Supérieur
- Sujet: fonction plusieur variables
- Réponses: 7
- Vues: 661
Bonjour, j'ai une petite question
dans un exercice j'ai une fonction g(t)
et dans la 1ere question, je dois montrer qu'elle est prolongeable par continuité en 0 en posant X=1/t
donc je l'ai fais et du coup ma fonction pour la suite est g(1/x) ? ou toujours g(t) ?
- par Raphoul
- 01 Juin 2014, 14:42
-
- Forum: ✯✎ Supérieur
- Sujet: fonction
- Réponses: 2
- Vues: 345
zygomatique a écrit:salut
ben si tu les avais, c'est que tu ne les a plus ... donc yaplus de pb ...
:ptdr:
ahah très drôle ^^, mais mon problème n'est pas toujours pas résolu,
- par Raphoul
- 14 Mai 2014, 20:11
-
- Forum: ✯✎ Supérieur
- Sujet: espace vectoriel
- Réponses: 3
- Vues: 433
Bonsoir,
je travail dans

j'avais F,G, j'ai démontrer que F et G étaient des s-ev de

j'ai de plus trouver une base de F et une base de G,
je dois montrer maintenant que

je ne sais pas comment faire.
Merci pour votre aide
- par Raphoul
- 14 Mai 2014, 20:05
-
- Forum: ✯✎ Supérieur
- Sujet: espace vectoriel
- Réponses: 3
- Vues: 433
salut la fonction f : t \rightarrow \dfrac {e^{-t}}{t} est continue sur {t > 0} donc elle admet des primitives soit F une primitive (qui est donc dérivable) sur {t > 0} alors pour x > 0 G(x) = F(2x) - F(x) et G'(x) = 2f(2x) - f(x) = ... j'ai bien compris qu'il fallait que je fasse a un moment donné...
- par Raphoul
- 06 Mai 2014, 19:52
-
- Forum: ✯✎ Supérieur
- Sujet: intégrale et dérivée
- Réponses: 9
- Vues: 880
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_fondamental_de_l'analyse Une petite manipulation sur l'intégrale, et vous pouvez utiliser le théorème fondamental. je connais le théorème fondamentale enfin je l'ai dans mon cours, au début j'ai pensé qu'il faudrait remplacer les "t" par &qu...
- par Raphoul
- 06 Mai 2014, 17:41
-
- Forum: ✯✎ Supérieur
- Sujet: intégrale et dérivée
- Réponses: 9
- Vues: 880
bonjour, j'ai la fonction G définie sur \mathbb{R}^{*}_{+} par : G(x)=\int_{x}^{2x} \frac{e^{-t}}{t} \, \mathrm{d}t \ Je dois démontrer que G est dérivable sur \mathbb{R}^{*}_{+} et que l'on a : \forall x \in \mathbb{R} , G'(x)=\frac{e^{-2x}(1-e^x)}{x} je sais pas comment...
- par Raphoul
- 06 Mai 2014, 16:52
-
- Forum: ✯✎ Supérieur
- Sujet: intégrale et dérivée
- Réponses: 9
- Vues: 880
zygomatique a écrit:quel est le dl de ln(1 + x) ?
)
(ordre 2)
- par Raphoul
- 05 Mai 2014, 19:36
-
- Forum: ✯✎ Supérieur
- Sujet: limite
- Réponses: 9
- Vues: 551
zygomatique a écrit:non pas pour cette raison ...
bah je sais pas alors
- par Raphoul
- 05 Mai 2014, 19:32
-
- Forum: ✯✎ Supérieur
- Sujet: limite
- Réponses: 9
- Vues: 551
zygomatique a écrit:à toi de voir ... :lol3: ... mais il semble évident d'aller au moins à ....
j'hésite entre 2 et 3... aller je pense a 2 a cause du carré en bas
- par Raphoul
- 05 Mai 2014, 19:19
-
- Forum: ✯✎ Supérieur
- Sujet: limite
- Réponses: 9
- Vues: 551
zygomatique a écrit:salut
dl de ln(1 + x) puis développement du numérateur ....
d'accord merci, jusqu'à quel ordre le dl ?
- par Raphoul
- 05 Mai 2014, 19:09
-
- Forum: ✯✎ Supérieur
- Sujet: limite
- Réponses: 9
- Vues: 551
bonjour, j'ai
=\frac{x-(1+x)ln(1+x)}{x^2(1+x)})
je veux calculer

)
j'ai bien vu qu'il y avait une forme indéterminé 0/0 mais je n'arrive pas à la lever
- par Raphoul
- 05 Mai 2014, 17:58
-
- Forum: ✯✎ Supérieur
- Sujet: limite
- Réponses: 9
- Vues: 551
Bonjour ! Tu as fait une erreur : ce n'est pas I_{3}-M=(I_{3}-M)(M^2+M+I_{3}) mais I_{3}-M^3=(I_{3}-M)(M^2+M+I_{3}) . Du coup tu peux simplifier (vu que tu as calculé M^3 ), et tu vas voir aussitôt l'inverse demandée. Au cas où tu ne verrais toujours pas (mais à mon ...
- par Raphoul
- 30 Mar 2014, 13:02
-
- Forum: ✯✎ Supérieur
- Sujet: matrice
- Réponses: 3
- Vues: 296
Bonjour on considère la matrice M = \begin{pmatrix}8&10&-6\\ -2&-3&1\\ 6&7&-5\\ \end{pmatrix} je devais calculer M^2 que j'ai fait et je trouve M^2 = \begin{pmatrix}8&8&-8\\ -4&-4&4\\ 4&4&-4\\ \end{pmatrix} et ensuite M^3 = \begin{pmatrix}0&0&0...
- par Raphoul
- 30 Mar 2014, 12:24
-
- Forum: ✯✎ Supérieur
- Sujet: matrice
- Réponses: 3
- Vues: 296
wserdx a écrit:Je t'ai proposé d'écrire -16 en forme polaire, c'est à dire trouver

et

tels que

. Sais-tu le faire?
oui ça fais

- par Raphoul
- 14 Mar 2014, 18:11
-
- Forum: ✯✎ Supérieur
- Sujet: Polynôme
- Réponses: 9
- Vues: 656
je ne vois pas trop comment partir
je sais qu'il faut que je résolve P(x)=0
je remplace P(x) par sa valeur mais je ne vois pas après
- par Raphoul
- 14 Mar 2014, 15:11
-
- Forum: ✯✎ Supérieur
- Sujet: Polynôme
- Réponses: 9
- Vues: 656
Bonjour,
je dois chercher, en remarquant que 16 est une puissance de 2, les racines du polynôme
=X^4+16)
Donner alors une factorisation dans C[X] et R[X] de P(X) en produit de polynôme irréductibles.
Donc j'écris
=X^4+2^4)
mais après je ne sais pas comment faire
- par Raphoul
- 14 Mar 2014, 14:44
-
- Forum: ✯✎ Supérieur
- Sujet: Polynôme
- Réponses: 9
- Vues: 656
