Fonction plusieur variables
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Raphoul
- Membre Relatif
- Messages: 139
- Enregistré le: 30 Oct 2013, 11:14
-
 par Raphoul » 19 Mar 2015, 17:22
par Raphoul » 19 Mar 2015, 17:22
Bonjour
je bloque sur une question d'un exercice
j'ai :

de classe

. On pose pour
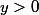
=h(\frac{x}{y}))
je dois déterminer

l'ensemble de définition de f
je ne sais pas comment faire
merci
-
Raphoul
- Membre Relatif
- Messages: 139
- Enregistré le: 30 Oct 2013, 11:14
-
 par Raphoul » 19 Mar 2015, 17:32
par Raphoul » 19 Mar 2015, 17:32
et ensuite je dois montrer que

h vérifie
h''(t)-2h'(t)=t)
avec


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 19 Mar 2015, 19:15
par zygomatique » 19 Mar 2015, 19:15
salut
h est définie sur ]0, 1[ et y > 0 donc il faut 0 < x/y < 1 ...
ensuite dérivée de fonctions composées ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Raphoul
- Membre Relatif
- Messages: 139
- Enregistré le: 30 Oct 2013, 11:14
-
 par Raphoul » 19 Mar 2015, 19:46
par Raphoul » 19 Mar 2015, 19:46
zygomatique a écrit:salut
h est définie sur ]0, 1[ et y > 0 donc il faut 0 < x/y < 1 ...
ensuite dérivée de fonctions composées ...
pour calculer les dérivées partielles seconde de f je passe par les dérivées partielles de h en utilisant la dérivée composé ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 19 Mar 2015, 21:30
par Pythales » 19 Mar 2015, 21:30
Raphoul a écrit:pour calculer les dérivées partielles seconde de f je passe par les dérivées partielles de h en utilisant la dérivée composé ?
Soit
=h(t))
avec
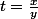
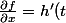\frac1{y^2})
\frac1{y^2})
(-\frac x{y^2}))
etc ...

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 19 Mar 2015, 23:31
par chombier » 19 Mar 2015, 23:31
faute de frappe :
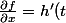\frac1{y} = \frac1{y}h'(\frac xy))

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Mar 2015, 09:54
par zygomatique » 20 Mar 2015, 09:54
Raphoul a écrit:pour calculer les dérivées partielles seconde de f je passe par les dérivées partielles de h en utilisant la dérivée composé ?
il n'y a pas de dérivée partielle pour h !!!! (fonction d'une variable !!!!)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 20 Mar 2015, 10:20
par Pythales » 20 Mar 2015, 10:20
chombier a écrit:faute de frappe :
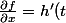\frac1{y} = \frac1{y}h'(\frac xy))
Exact. Merci.
La dérivée seconde est exacte...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités