Intégrale et dérivée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Raphoul
- Membre Relatif
- Messages: 139
- Enregistré le: 30 Oct 2013, 11:14
-
 par Raphoul » 06 Mai 2014, 16:52
par Raphoul » 06 Mai 2014, 16:52
bonjour,
j'ai la fonction G définie sur
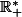
par :
=\int_{x}^{2x} \frac{e^{-t}}{t} \, \mathrm{d}t \)
Je dois démontrer que G est dérivable sur
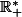
et que l'on a :
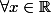
,
=\frac{e^{-2x}(1-e^x)}{x})
je sais pas comment m'y prendre pour dérivé, j'ai essayé plusieurs choses telle que dérivé

ou calculer l'intégrale, et d'autre trucs, mais j'avance pas
Je voudrai savoir comment démarrer svp
-
Axel2L
- Messages: 3
- Enregistré le: 06 Mai 2014, 13:07
-
 par Axel2L » 06 Mai 2014, 17:33
par Axel2L » 06 Mai 2014, 17:33
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_fondamental_de_l'analyse
Une petite manipulation sur l'intégrale, et vous pouvez utiliser le théorème fondamental.
-
Raphoul
- Membre Relatif
- Messages: 139
- Enregistré le: 30 Oct 2013, 11:14
-
 par Raphoul » 06 Mai 2014, 17:41
par Raphoul » 06 Mai 2014, 17:41
Axel2L a écrit:http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_fondamental_de_l'analyse
Une petite manipulation sur l'intégrale, et vous pouvez utiliser le théorème fondamental.
je connais le théorème fondamentale enfin je l'ai dans mon cours, au début j'ai pensé qu'il faudrait remplacer les "t" par "x" mais je ne pense pas que c'est sa
le changement de variable peut etre ?
-
Axel2L
- Messages: 3
- Enregistré le: 06 Mai 2014, 13:07
-
 par Axel2L » 06 Mai 2014, 17:52
par Axel2L » 06 Mai 2014, 17:52
Oui, il faut faire une manipulation avant.
Pourquoi ne pouvez-vous pas utiliser le théorème fondamental ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 06 Mai 2014, 17:59
par zygomatique » 06 Mai 2014, 17:59
salut
la fonction

est continue sur {t > 0} donc elle admet des primitives
soit F une primitive (qui est donc dérivable) sur {t > 0}
alors pour x > 0 G(x) = F(2x) - F(x) et G'(x) = 2f(2x) - f(x) = ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Raphoul
- Membre Relatif
- Messages: 139
- Enregistré le: 30 Oct 2013, 11:14
-
 par Raphoul » 06 Mai 2014, 19:52
par Raphoul » 06 Mai 2014, 19:52
zygomatique a écrit:salut
la fonction

est continue sur {t > 0} donc elle admet des primitives
soit F une primitive (qui est donc dérivable) sur {t > 0}
alors pour x > 0 G(x) = F(2x) - F(x) et G'(x) = 2f(2x) - f(x) = ...
j'ai bien compris qu'il fallait que je fasse a un moment donné F(2x)-F(x)
après je ne comprend pas le 2f(2x) ni après ce qu'il faut faire..., j'ai essayé de mettre 2x a la place de t et x a la place de t aussi de la même façon...

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 06 Mai 2014, 20:27
par eratos » 06 Mai 2014, 20:27
Raphoul a écrit:j'ai bien compris qu'il fallait que je fasse a un moment donné F(2x)-F(x)
après je ne comprend pas le 2f(2x) ni après ce qu'il faut faire..., j'ai essayé de mettre 2x a la place de t et x a la place de t aussi de la même façon...
u(x)=2x
(Fou(x))'=u'(x)F'ou(x)
Pour le reste, tu factorises 2f(2x) -f(x) . :lol3:
Enfin, tu te dis qu'une fonction dont la dérivée est partout continue est partout dérivable.
-
Pas-fort
- Messages: 2
- Enregistré le: 10 Mai 2014, 17:28
-
 par Pas-fort » 10 Mai 2014, 17:39
par Pas-fort » 10 Mai 2014, 17:39
Bonjour,
Désoler d'utiliser une conversation déjà entamer mais je suis tout nouveau et je sais pas comment utiliser ce forum pour le moment,
Si je suis ici c'est que j'ai besoin de votre aider
Je m'appelle LOIC et je suis en BTS électrotechnique comme c'est bientôt la fin de l'année et bientôt les examen donc je révise les annales
je suis tomber sur une integrale simple a faire mais que je comprend pas
f(t) = 0.5t +0.5 si -1f(t) = 0.5
il faut faire l'intergale de f(t) sur -1à 1
sauf que dans le corrigé il font de cette manière
integrale de -1 à 1 de 0.5(t-1) dt
0.5t + 0.5 = 0.5(t+1) si on factorise alors que dans le corriger c pas le cas
merci d'avance

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 10 Mai 2014, 18:31
par eratos » 10 Mai 2014, 18:31
Pas-fort a écrit:Bonjour,
Désoler d'utiliser une conversation déjà entamer mais je suis tout nouveau et je sais pas comment utiliser ce forum pour le moment,
Si je suis ici c'est que j'ai besoin de votre aider
Je m'appelle LOIC et je suis en BTS électrotechnique comme c'est bientôt la fin de l'année et bientôt les examen donc je révise les annales
je suis tomber sur une integrale simple a faire mais que je comprend pas
f(t) = 0.5t +0.5 si -1<t<1
f(t) = 0.5
il faut faire l'intergale de f(t) sur -1à 1
sauf que dans le corrigé il font de cette manière
integrale de -1 à 1 de 0.5(t-1) dt
0.5t + 0.5 = 0.5(t+1) si on factorise alors que dans le corriger c pas le cas
merci d'avance
ils se sont trompés dans le corrigé :lol3:
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 13 Mai 2014, 14:05
par deltab » 13 Mai 2014, 14:05
Bonjour
Pas-fort a écrit:f(t) = 0.5t +0.5 si -1<t<1
f(t) = 0.5
Énoncé incomplet:
f(t)=0.5 pour t=??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
est continue sur {t > 0} donc elle admet des primitives