10 résultats trouvés
Revenir à la recherche avancée
- 02 Jan 2011, 21:21
- Forum: ✎✎ Lycée
- Sujet: [DM] Nombres complexes 1ere STI EL
- Réponses: 13
- Vues: 979
Oui c'est bon, le résultat devient bien i(x-y-2)+3+x+y Pour la suite je pense avoir compris, ce serait juste pour une vérification : La question suivant, on nous demande de déduire que la résolution de (E1) conduit à un système de deux équations d'inconnues x et y à résoudre. J'ai décidé d'a...
- 02 Jan 2011, 20:43
- Forum: ✎✎ Lycée
- Sujet: [DM] Nombres complexes 1ere STI EL
- Réponses: 13
- Vues: 979
Donc je fait pour le 1 : (1+i)x-iy +3 -2i, je développe le tout, et je factorise par i ?
Et sinon pour l'autre question, je vois à peu près comment faire, merci :lol3:
Edit : Le calcul me donne :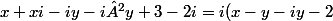+3+x) , c'est bon ?
, c'est bon ?
Et sinon pour l'autre question, je vois à peu près comment faire, merci :lol3:
Edit : Le calcul me donne :
- 02 Jan 2011, 20:11
- Forum: ✎✎ Lycée
- Sujet: [DM] Nombres complexes 1ere STI EL
- Réponses: 13
- Vues: 979
Oui, pour le 1) on est mal barré :ptdr: Donc ce serait z= \overline{z} + i\overline{z} + 3 - 2i le calcul total ? Néanmoins, la question surment la plus bête mais qui me perturbe : Comment on saurait \overline{z} alors que ce dernier est compris dans l'équation de z ? Et sinon, pour la formule de Z1...
- 02 Jan 2011, 19:25
- Forum: ✎✎ Lycée
- Sujet: [DM] Nombres complexes 1ere STI EL
- Réponses: 13
- Vues: 979
Pour l'exercice 2 du 1, le z barre, je l'utilise pour le 1 +i ? ( ce qui donnerait 1 - i) ? Pour l'application numérique, c'est une autre question à cotée (petit 2) où j'ai z²+2z+2=0 Donc delta = 4-8=-4 Donc z1 = \frac{-2-i sqrt {-4}}{1} donc = -2-i sqrt {-4} Et z2= \frac{-2+i sqrt {-4}}{1} donc = -...
- 02 Jan 2011, 18:56
- Forum: ✎✎ Lycée
- Sujet: [DM] Nombres complexes 1ere STI EL
- Réponses: 13
- Vues: 979
- 02 Jan 2011, 17:39
- Forum: ✎✎ Lycée
- Sujet: Blocage exercice 1ere STI EL.
- Réponses: 3
- Vues: 747
[DM] Nombres complexes 1ere STI EL
Bonsoir tout le monde. J'aurait besoin de votre aide pour 2 questions d'un DM à faire : Exercice 02. On considère dans C léquation (E1) dinconnue z : (E1) : z= (1 + i)z barre + 3 - 2i où z = x + iy avec x et y appartenants à R 1. Calculer en fonction de x et de y les parties réelles et imaginaires...
- 02 Jan 2011, 17:32
- Forum: ✎✎ Lycée
- Sujet: [DM] Nombres complexes 1ere STI EL
- Réponses: 13
- Vues: 979
- 02 Jan 2011, 15:24
- Forum: ✎✎ Lycée
- Sujet: Blocage exercice 1ere STI EL.
- Réponses: 3
- Vues: 747
- 02 Jan 2011, 12:41
- Forum: ✎✎ Lycée
- Sujet: Blocage exercice 1ere STI EL.
- Réponses: 3
- Vues: 747
Blocage exercice 1ere STI EL.
Bonjour tout le monde. J'ai un petit blocage sur 2 questions d'un exercice (qui n'est pas dans un DM) et j'aurait besoin d'aide :we: Tout d'abord, voici l'énoncé : Soit f la fonction définie sur [0; + infinis] par f(x) = Racine de x. On note Cf sa courbe représentative dans un repère orthogonal ( Un...
- 02 Jan 2011, 08:37
- Forum: ✎✎ Lycée
- Sujet: Blocage exercice 1ere STI EL.
- Réponses: 3
- Vues: 747
- 10 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
