8 résultats trouvés
Revenir à la recherche avancée
Ericovitchi a écrit:tu fais un tableau méthodique en examinant tous les cas
x=0 --> y>0 --> z0 --> y z=0
x soit y>0 --> z=0
soit y=0 --> z>0
soit y z=0
j pas compris c'est possile solution et merci
- par anoir dsr
- 03 Oct 2010, 14:01
-
- Forum: ✯✎ Supérieur
- Sujet: Problem
- Réponses: 7
- Vues: 910
Ericovitchi a écrit:tu es sûr de P3 car " y 6= 0

" c'est bizarre. c'est quoi y 6 ? il doit manquer un signe
P3 : y = 0

z > 0.
- par anoir dsr
- 03 Oct 2010, 13:47
-
- Forum: ✯✎ Supérieur
- Sujet: Problem
- Réponses: 7
- Vues: 910
Bonjour, je ne sais pas comment traiter cette question Soit x, y et z trois r´eels parmi lesquels il y a z´ero et deux r´eels non nuls de signe contraire. On suppose que les trois implications suivantes sont vraies : P1 : x = 0 ;) y > 0 P2 : x > 0 ;) y < 0 P3 : y = 0 ;) z > 0. Comparer x, y et z.
- par anoir dsr
- 03 Oct 2010, 02:03
-
- Forum: ✯✎ Supérieur
- Sujet: Problem
- Réponses: 7
- Vues: 910


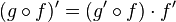
" c'est bizarre. c'est quoi y 6 ? il doit manquer un signe