Forum de Mathématiques: Maths-Forum

ah, je n'ai pas eu d'accès à internet depuis, bref... Avec le AF/AK = e j'ai obtenu que l'abssice de A était 2, il se situe sur l'axe focal donc pour le point A ça doit être bon... Mais je bloque sur les autres indications qui m'ont été fournies sur a, b et c... enfin je ne peux pas les déterminer c...

Merci beaucoup je regarde ça...
Mais le point A est forcément entre K et F ?

Bonjour, j'ai un problème de compréhension au niveau des coniques et un exercice pourrait m'aider à avancer je pense... Voici les information dont je dispose : la conique C a pour foyer F :(1,-1) pour directrice D : x = 5 et pour excentricité e = 1/3 Question 1 : Déterminer la nature de C, l'axe foc...

Ah d'accord, il y a 4 cas différent donc,

un vecteur (a,b) avec a et b non nuls,
un vecteur (a,0) avec a non nul
un vecteur (0,b) avec b non nul
et le cas (0,0)

l'ensemble des g.x pour x=(12,-27) si g parcourt le groupe G sera \ ... Donc la on a trouvé l'orbite de tout point ...
Et maintenant je doit chercher l'orbite de (0,0) c'est ça ?

Bonsoir, Je n'arrive pas à comprendre comment trouver les orbites d'une action de groupe, je me disais donc qu'un exemple expliqué pourrait peut-être rendre la notion plus claire à mes yeux : On fait agir G = \left\{ \begin{pmatrix} a & 0 \\ 0 & b \end{matrix} | a \neq 0, b \neq 0 \right\} s...

On fixe un x_0 appartenant, à \mathbb{R} , on veut montrer que \bigsum f_n(x) est absolument convergente, on étudie donc \bigsum |f_n| = \bigsum \frac{1}{x_0^2 + n} ... J'avais déjà essayé comme ça mais je bloque ( enfin si c'est bien l'idée que tu proposais ...) ici ... Je pense que je dois...

Bonjour,

Je dois chercher le domaine de convergence D de la sére de fonction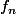 avec et je suis un peu bloqué...

Quelqu'un pourrait me donner un petit indice pour que je sache par ou commencer ?

Merci d'avance...

... xD, effectivement, on ne peut pas avoir (1/n,0) = (0,0) pour n={1,2,.... }
Merci beaucoup ^^

Bonjour, Je cherche à comprendre pourquoi le sous-ensemble de \mathbb{R}^2 : A = \{ (\frac{1}{n},0); n = 1, 2, ... \} n'est pas fermé. Je dois mal comprendre la notion d'adhérence car pour moi l'adhérence de A est bien égale à A => A est fermé ... :hum: Enfin bref, si quelqu'un pouvait m'écl...