Forum de Mathématiques: Maths-Forum

En effet, je te remercie pour ton aide. je n'est plus qu'a interpréter tout cela de facon economique pour mon exercice :we:

Mais j'ai aussi q= 0.12/0.3 ou pas ?

Ok alors j'ai Delta = -8.9856+0.6p Soit pour p=14.976 delta = 0 Donc Une racine --> 0.12/0.3 Si p14.976 deux racines ---> 0.12-sqrt{Delta}/ 0.3 et 0.12+sqrt{Delta}/ 0.3 je ne crois pas qu'il y est d'erreurs de calculs. Mais je ne constate pas que c'est directement ce que je veux. ( certainement que ...

D'accord, ca j'ai compris. Mais aurais-je à la fin quelque chose de la forme f(p)=q ?
Désolé si je n'est pas était clair précédement

Mais cette fonction n'est pas égale a 0 mais à P. Cela ne change rien ?

Ou sinon je peux peut étre faire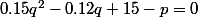 ? Mais aprés comment je détermine Q en fonction de p ?

Bonsoir.

J'aurais aimé un petit coup de main, je dois dans cette équation exprimer Q en focntion de P, mais impossible. Je ne sais pas pourquoi je n'y arrive pas.
Merci d'avance.

Merci bien a vous.

je considére donc K comme un nombre réel ? et je dérive normalement ?

Soit = 2 ?

Bonsoir , ma question est qu'est ce qu'une dérivée partielle ?

je sait qu'on l'écrit par exemple pour une fonction qui serais par exemple F=K+2L

Mais que dois-je calculer ? Quelle est la méthode ?
Je vous remercie.

Bonsoir , tu dois juste appliquer la formule de la tangente au point d'abscisse 0.

l'équation étant y = f '(a) (x - a) + f(a)

Je vous remercie pour ces précisions , c'est beaucoup plus clair maintenant.

Voila l'énoncé tout d'abord Soit f l'application définie sur R \ {1} par f(x) = (3x-1)/(x-1) Démontrer que f est une bijection de R \ {1} sur une partie de R qu'on precisera et donner l'expression de f^-1 j'ai bien entendu commencer l'exercice , si on appel F la partie de R , pour que f soit bijecti...

Bonsoir, je voudrais savoir comment commencer ma demonstration

je dois demontrer que la somme de deux fonction pair et pair

J'ai établie deux foncion pair soit F et G

Mais je bloque pour commencer ..

Merci d'avance :marteau:

(25-36)+(36-49)+(49-64)

donc cela revient a faire 25 - 64 dans ce cas la

soit (5²-(5+1)²) - ((n-3)²-((n-3+1)²)

et je simplifie cela ?

Bonsoir à tous, j'aimerais un petit coup de main pour un exercice sur lequel , je plante complétement

enoncé : Calculer en utilisant le principe du télescopage

le E étant le symbole de la somme


n-3
E (k²- (k+1)²)
k=5


je ne comprend pas ce qu'il faut faire ... Meci d'avance

a voila !, c'est ce que je n'arrivait pas à faire, aprés tout devient logique , je vous remercie.

j'ai une autre question ... ( je sui svraiment pas doué en trigo )

je devais exprimer cos3x*cosx en fonction de cos^4x et cos²x

soit :

j'en arrive à

(2cos^3x - cosx -( 2sinx * cosx) *sinx ) * cosx

j'aimerai sbien faire disparaitre les sinx , comment faire ?

Merci bien

sa me fait cos²x -sin²x +2sin²x
= cos²x +sin²x
=1
la constante est donc 1 ?

j'ai trouvé la reponse en faisant

(cos²x + sin²x )(cos²x - sin²x)+2sin²x

(cos²x)² - (sin²x)² + 2sin²x

= (cos² - sin²x )² - (sin²x)² +2sin²x
= ((1-sin²x)-sin²x)² - ( sin²x)² +2 sin²x

Bien partit ou pas ?

( 1 -2sin²x)² -(sin²x)² + 2 sin²x

une fois la je vois pas trop , mais je voudrait savoir si c'est la bonne suite ?