Fonction bijective.

[grymist]

Voila l'énoncé tout d'abord

Soit f l'application définie sur R \ {1} par f(x) = (3x-1)/(x-1)
Démontrer que f est une bijection de R \ {1} sur une partie de R qu'on precisera et donner l'expression de f^-1


j'ai bien entendu commencer l'exercice , si on appel F la partie de R , pour que f soit bijective les conditions sont :

pour y appartient a F il existe x qui appartient a R \ {1} tel que y = f(x)
et que pour y appartient a F il existe x qui appartient a R \ {1} tel que y = (3x-1)/(x-1)
--> donc je résoute y=(3x-1)/(x-1) ?
si c'est le cas je bloque , sinon les conditions que je pose sont elles les bonnes ? je vous remercie !

[Ericovitchi]

Pour qu'elle soit bijective, il faut surtout qu'elle soit monotone et que l'image soit R tout entier. Donc étudie la fonction et montre qu'elle est toujours décroissante, que ses limites vont jusqu'à + et - l'infini (au voisinage de 1) et donc que tout point a une image (sauf x=1) et réciproquement.

Pour le réciproquement et pour trouver tu poses y=(3x-1)/(x-1) et tu exprimes x en fonction de y.

[kasmath]

il y'a deux méthodes de résoudre cet exercice la pre c'est d'étudier la fonction il faut montrer qu'elle-est montone et continue sur R-1 donc elle est bijictive et pour trouver l'expression de 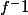tu pose et tu considère x comme réel fixe ou tu dois le difinire sa appartenance par contre y comme un variable de r-1 et tu résoudre l'équation



la deusième méth . c'est de montrer que f est injéctive et surjéctive et pour trouver l'expression de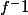 tu pose f(y)=x et tu considère x comme réel fixe ou tu dois le difinire sa appartenance par contre y comme un variable de r-1 et tu résoudre l'équation

[grymist]

Je vous remercie pour ces précisions , c'est beaucoup plus clair maintenant.