35 résultats trouvés
Revenir à la recherche avancée
- 14 Sep 2010, 09:00
- Forum: ✯✎ Supérieur
- Sujet: polynomes de Legendre
- Réponses: 16
- Vues: 1714
- 13 Sep 2010, 19:13
- Forum: ✯✎ Supérieur
- Sujet: polynomes de Legendre
- Réponses: 16
- Vues: 1714
bonjour, je pense avoir quelques pistes 1) Montrer qu'il existe (\lambda_0,...,\lambda_n) \in \mathbb{R}^{n+1} tel que L_n(-X-1) = \lambda_0 L_0 + ... + \lambda_nL_n idée : utiliser le fait que L_n a n racines simples dans ]-1,0[ ? 2) Etablir l'égalité : L_n(-X-1) = (-1&#...
- 13 Sep 2010, 10:08
- Forum: ✯✎ Supérieur
- Sujet: polynomes de Legendre
- Réponses: 16
- Vues: 1714
- 12 Sep 2010, 22:23
- Forum: ✯✎ Supérieur
- Sujet: Démonstration
- Réponses: 20
- Vues: 1358
- 12 Sep 2010, 22:13
- Forum: ✯✎ Supérieur
- Sujet: Démonstration
- Réponses: 20
- Vues: 1358
- 12 Sep 2010, 22:09
- Forum: ✯✎ Supérieur
- Sujet: Démonstration
- Réponses: 20
- Vues: 1358
- 12 Sep 2010, 22:04
- Forum: ✯✎ Supérieur
- Sujet: Démonstration
- Réponses: 20
- Vues: 1358
- 12 Sep 2010, 21:48
- Forum: ✯✎ Supérieur
- Sujet: polynomes de Legendre
- Réponses: 16
- Vues: 1714
- 12 Sep 2010, 21:43
- Forum: ✯✎ Supérieur
- Sujet: Démonstration
- Réponses: 20
- Vues: 1358
- 12 Sep 2010, 21:40
- Forum: ✯✎ Supérieur
- Sujet: polynomes de Legendre
- Réponses: 16
- Vues: 1714
- 12 Sep 2010, 21:21
- Forum: ✯✎ Supérieur
- Sujet: polynomes de Legendre
- Réponses: 16
- Vues: 1714
Bonsoir, oui tu as l'idée c'est bien mais tu peux utiliser d'emblée : \sqrt{ab} \leq \frac{a+b}{2} Pourquoi ? car tu sais aussi que \ln{\sqrt{a}} = \frac{1}{2} \ln a La fonction ln est strictement croissante sur ]0,+\infty[ (important à dire car ainsi tu conserves l'ordre de ton inéquation) donc : l...
- 12 Sep 2010, 20:44
- Forum: ✯✎ Supérieur
- Sujet: Démonstration
- Réponses: 20
- Vues: 1358
yes en fait je m'en suis rendu compte y a l'expression de la dérivée d'un produit dans l'équation, ça roule tout seul, sinon bah c'est impossible ce truc lol ! Thanks !
- 12 Sep 2010, 17:05
- Forum: ✯✎ Supérieur
- Sujet: polynomes de Legendre
- Réponses: 16
- Vues: 1714
Bonjour,
^2)
c'est une identité remarquable donc tu sais développer ça facilement et il te faudra utiliser le fait que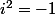 . Ensuite mettre sous forme algébrique un complexe c'est l'avoir de la forme
. Ensuite mettre sous forme algébrique un complexe c'est l'avoir de la forme 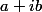
c'est une identité remarquable donc tu sais développer ça facilement et il te faudra utiliser le fait que
- 12 Sep 2010, 16:55
- Forum: ✎✎ Lycée
- Sujet: Forme algébrique de nombre complexe
- Réponses: 6
- Vues: 1018
Bon on est donc arrivé à ^2 = \alpha + 2i\beta)
Si on passe au module on va avoir :

soit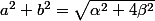
De plus on sait que :
En faisant la somme des deux on va peut être expliciter tout ça..
Si on passe au module on va avoir :
soit
De plus on sait que :
En faisant la somme des deux on va peut être expliciter tout ça..
- 12 Sep 2010, 16:32
- Forum: ✯✎ Supérieur
- Sujet: j'y est passé ma journée
- Réponses: 7
- Vues: 678
Bonjour merci beaucoup d'avoir pris le temps de vérifier je suis arrivé à ça aussi :). En fait je doutais parce qu'il va falloir que je l'utilise dans la partie 2 pour démontrer que : n(n+1) = m(m+1) où en fait c'est un produit scalaire de \mathbb{R}[X] définit ainsi : = \int_{-1}^{0...
- 12 Sep 2010, 16:09
- Forum: ✯✎ Supérieur
- Sujet: polynomes de Legendre
- Réponses: 16
- Vues: 1714
- 12 Sep 2010, 15:33
- Forum: ✯✎ Supérieur
- Sujet: j'y est passé ma journée
- Réponses: 7
- Vues: 678
- 35 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
