Polynomes de Legendre

[romi64]

Bonjour j'aimerai que vous me dites si mes résultats d'une partie d'un problème sont justes, le sujet est le suivant :

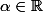
Pour , on note l'équation différentielle :



Soit

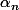
1) Déterminer la valeur de , que l'on notera , telle que possède au moins une solution polynomiale à coefficients réels et de degré exactement égal à n.

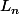
2) Montrer que possède une unique solution polynomiale, notée , à coefficients réels de degré exactement égal à n et telle que

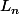
3) Expliciter les coefficients de à l'aide de coefficients binomiaux. (On pourra remarquer que


Réponses

1) On trouve

2) On utilise le théorème de Cauchy - Lipschitz mais j'ai du mal à justifier proprement.

3) En posant , je trouve :



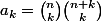
sans aucune certitude ... ai-je fais des erreurs ?

Merci

[girdav]

Bonjour,
j'arrive au lien de récurrence , et ce que tu donnes semble vérifier cela.

[romi64]

Bonjour merci beaucoup d'avoir pris le temps de vérifier je suis arrivé à ça aussi . En fait je doutais parce qu'il va falloir que je l'utilise dans la partie 2 pour démontrer que :



où en fait c'est un produit scalaire de définit ainsi :



ça m'a l'air tendu s'il faut que je passe par des produits de somme et tout :marteau: . Qu'en penses tu?

Merci beaucoup !

[girdav]

Je ne crois pas que ça soit nécessaire. On peut utiliser le fait que .

[romi64]

yes en fait je m'en suis rendu compte y a l'expression de la dérivée d'un produit dans l'équation, ça roule tout seul, sinon bah c'est impossible ce truc lol ! Thanks !

[girdav]

Pour la question deux en fait comme on a établi l'existence à la question 1 il suffit de montrer l'unicité. On montre que si et sont solutions de alors , qui est encore solution, est le polynôme nul. On peut le faire en dérivant l'équation et en procédant par récurrence.

[romi64]

Oui bonne idée !

Maintenant je bataille à démontrer que

[girdav]

As-tu fait la sous-question précédente?

[romi64]

ah celle où il faut montrer que Ln(-1-X) s'écrit comme combinaison linéaire de ?

[girdav]

ah celle où il faut montrer que Ln(-1-X) s'écrit comme combinaison linéaire de ?

Oui, apparemment l'énoncé veut nous faire comprendre que l'on doit s'en servir.

[romi64]

Bah faut utiliser que est un base, après le lien entre les deux je sais pas encore comment le faire

[romi64]

bonjour, je pense avoir quelques pistes

1) Montrer qu'il existe tel que

idée : utiliser le fait que a n racines simples dans ]-1,0[ ?

2) Etablir l'égalité :

idée : utiliser 1) et faire récurrence sur n ?

Qu'en penses tu Girdav?

[girdav]

Bonjour,
je pense qu'il faut se servir du fait que la base est orthogonale : on peut ainsi voir que pour on a , puisque chaque est dans . Il ne reste donc qu'à évaluer , ce qui peut se faire par une comparaison des coefficients dominants.

[romi64]

Bonsoir,

implique que :

= + ?

[girdav]

En fait, on peut trouver des , pour tels que la famille soit une base orthonormée de . Il suffit de voir ce que sont les coordonnées du polynôme dans cette base.

[romi64]

je ne vois pas trop comment les trouver, dsl l'algèbre linéaire ça fait loin pour moi :triste:

[girdav]

Si est une base orthonormée d'un espace euclidien , alors pour tout vecteur de la forum on a .
On peut le voir en calculant le produit scalaire et en utilisant la linéarité.