Vu l'énoncé, peut-on considérer directement que y=e^{x} est une solution particulière et ainsi tirer la solution générale ?
11 résultats trouvés
Revenir à la recherche avancée
Oui, en effet, la solution de l'équation homogène est plutôt :
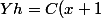)
Vu l'énoncé, peut-on considérer directement que y=e^{x} est une solution particulière et ainsi tirer la solution générale ?
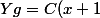 + e^{x})
Vu l'énoncé, peut-on considérer directement que y=e^{x} est une solution particulière et ainsi tirer la solution générale ?
- 01 Sep 2010, 18:55
- Forum: ✯✎ Supérieur
- Sujet: Equation différentielle d'ordre 1
- Réponses: 3
- Vues: 544
Rhaaa je suis encore bloqué... \HUGE(\rho e^{i\theta})^{3} + \overline{(\rho e^{i\theta})}^{3}=0\\ \rho^{3}e^{3i\theta}+\rho^{3}e^{-3i\theta}=0\\ \rho^{3}e^{3i\theta}(1+e^{-6i\theta})=0\\ Si on considère z différent de 0, \HUGE1+e^{-6i\theta}=0\\ e^{-6i\theta}=-1 Ce qui me se...
- 01 Sep 2010, 18:38
- Forum: ✎✎ Lycée
- Sujet: Encore une équation complexe !
- Réponses: 9
- Vues: 818
- 01 Sep 2010, 16:57
- Forum: ✎✎ Lycée
- Sujet: Encore une équation complexe !
- Réponses: 9
- Vues: 818
Donc, si je développe encore un peu,
(a-\sqrt{3}b) = 0)
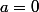
 = 0)
 = 0)
Si a = 0, alors b = 0, ne suis-je pas censé obtenir d'autres solutions ? :triste:
Si a = 0, alors b = 0, ne suis-je pas censé obtenir d'autres solutions ? :triste:
- 01 Sep 2010, 16:31
- Forum: ✎✎ Lycée
- Sujet: Encore une équation complexe !
- Réponses: 9
- Vues: 818
Equation différentielle d'ordre 1
Bonjour à tous, Je dois résoudre cette équation différentielle : g(x)y' - y = x e^{x} a) Trouver g(x) pour que y=e^{x} soit solution dans R. b) Trouver la solution générale avec g(x) trouvé en a). Pour trouver g(x) j'ai remplacé y dans l'ED et j'ai obtenu: g(x...
- 01 Sep 2010, 16:23
- Forum: ✯✎ Supérieur
- Sujet: Equation différentielle d'ordre 1
- Réponses: 3
- Vues: 544
Encore une équation complexe !
Re-Bonjour tout le monde ! :zen: Je dois résoudre l'équation z^{3} + \overline{z^{3}} = 0 Je pense que je peux appliquer la propriété qui dit que z + \overline{z} = 2 Re(z) D'où, si z = a + ib , 2a^{3} - 6 ab^{2} = 0 J'ai une seule équation à 2 inconnues, comment puis-je procéder pour la sui...
- 01 Sep 2010, 15:58
- Forum: ✎✎ Lycée
- Sujet: Encore une équation complexe !
- Réponses: 9
- Vues: 818
Ah, bien vu pour la factorisation !
C'est parce que j'ai un autre exercice du même type qui n'est pas factorisable de la même manière :
1 - i . z^2 = z - i
Ici, le delta vaut -3 + 4i et la résolution est facile !
Merci encore !
C'est parce que j'ai un autre exercice du même type qui n'est pas factorisable de la même manière :
1 - i . z^2 = z - i
Ici, le delta vaut -3 + 4i et la résolution est facile !
Merci encore !
- 01 Sep 2010, 15:45
- Forum: ✎✎ Lycée
- Sujet: Complexes, équation !
- Réponses: 8
- Vues: 1258
- 01 Sep 2010, 13:50
- Forum: ✎✎ Lycée
- Sujet: Complexes, équation !
- Réponses: 8
- Vues: 1258
Complexes, équation !
Bonjour tout le monde, Je dois déterminer les nombres complexes z:=a+ib avec a,b réels tels que iz + i = z^2 - 1 J'ai pensé à 2 méthodes pour résoudre, mais je doute de moi ! 1ere méthode) Traiter l'équation comme une équation du second degré z^2 - iz - 1 - i = 0 Le delta vaut : 5 + 4i et je cherche...
- 01 Sep 2010, 13:29
- Forum: ✎✎ Lycée
- Sujet: Complexes, équation !
- Réponses: 8
- Vues: 1258
- 30 Aoû 2010, 16:10
- Forum: ✎✎ Lycée
- Sujet: Exponentielle complexe
- Réponses: 5
- Vues: 737
Exponentielle complexe
Bonjour tout le monde, Je dois déterminer les nombres complexes z:=a+ib avec a,b réels tels que e^(iz) = 1 J'ai pensé décomposer de la manière suivante : J'ai d'abord posé z=a+ib e^(-b+ia)=1 Ensuite, e^(-b) . (cos a + i sin a) = 1 Partie réelle : e^(-b) . cos a = 1 (1) Partie imaginaire : e^(-b) . s...
- 30 Aoû 2010, 15:28
- Forum: ✎✎ Lycée
- Sujet: Exponentielle complexe
- Réponses: 5
- Vues: 737
- 11 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
