Je dois résoudre l'équation
Je pense que je peux appliquer la propriété qui dit que
D'où, si
J'ai une seule équation à 2 inconnues, comment puis-je procéder pour la suite ?
Encore une équation complexe !
10 messages
- Page 1 sur 1
Encore une équation complexe !
par poipoi » 01 Sep 2010, 15:58
Re-Bonjour tout le monde ! :zen:
Je dois résoudre l'équation
Je pense que je peux appliquer la propriété qui dit que
)
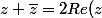D'où, si
,
J'ai une seule équation à 2 inconnues, comment puis-je procéder pour la suite ?
Je dois résoudre l'équation
Je pense que je peux appliquer la propriété qui dit que
D'où, si
J'ai une seule équation à 2 inconnues, comment puis-je procéder pour la suite ?
par poipoi » 01 Sep 2010, 16:31
Donc, si je développe encore un peu,
(a-\sqrt{3}b) = 0)
 = 0)
 = 0)
Si a = 0, alors b = 0, ne suis-je pas censé obtenir d'autres solutions ? :triste:
Si a = 0, alors b = 0, ne suis-je pas censé obtenir d'autres solutions ? :triste:
par MacManus » 01 Sep 2010, 16:36
L'équation s'écrit bien sous la forme (a-\sqrt{3}b)=0)
grossièrement si A*B*C=0 alors : soit A=0, soit B=0, soit C=0.
donc ici cela donne ?
tu obtiens trois solutions disjointes.
grossièrement si A*B*C=0 alors : soit A=0, soit B=0, soit C=0.
donc ici cela donne ?
tu obtiens trois solutions disjointes.
par Olympus » 01 Sep 2010, 16:40
Sauf erreur ( j'y ai pas retouché depuis longtemps ), ton équation admet une infinité de solutions . En fait, 0 et tout complexe dont l'argument est congru à 
modulo 
satisfont ton équation .
par poipoi » 01 Sep 2010, 18:38
Rhaaa je suis encore bloqué...
^{3} + \overline{(\rho e^{i\theta})}^{3}=0\\<br />\rho^{3}e^{3i\theta}+\rho^{3}e^{-3i\theta}=0\\<br />\rho^{3}e^{3i\theta}(1+e^{-6i\theta})=0\\)
Si on considère z différent de 0,
Ce qui me semble impossible ?
Si on considère z différent de 0,
Ce qui me semble impossible ?
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :