Forum de Mathématiques: Maths-Forum

Je trouve rien, je ne sais pas isoler z et ma constante?

Ok j'avais trouvé ce résultat en trouvant = avec une rotation basée sur le fait que la droite passe par 0 mais sa me semble louche,

Et pour la deuxième je mets un c alors?

Merci beaucoup

Doraki je ne comprends pas vraiment t'as méthode, je trouve

Si z appartient a une droite privée de O, alors c nul
je trouve (za+bar(z))/zbar(z) (Désole c'est un mac je sais pas comment faire l'antislash)

Moi j'avais essayé avec z= x+ikx avec k réel
mais je ne trouve rien de conclant...

Oai, mais je tombe alors sur un truc genre:

x'- = 0
y'- =0

Sa se rapproche d'une équation de cercle mais sa n'en ai pas une malheureusement.

Bonjour j'ai quelque petites questions: Soit I-> \frac{1}{conjuguée de z} 1) Déterminer l'image d'une droite passant par 0 privée de 0 Je trouve que sa correspond à a la meme droite, j'ai utilisé des rotations mais sa me semble faux car on me demande l'image d'un cercle et I°I(z)= Id, donc je pense ...

La formule à l'air sympa mais c'est pour un dm donc je pense que sa n'est pas la méthode voulue, je n'ai pas compris la première pouvais vous la réexpliquer?
Et oui la première question etait demontré la formule de machin.

Bonjour j'ai quelque petites questions: _ Trouver que \frac{\pi}{4} =12Arctan \frac{1}{18} +8Arctan \frac{1}{57} -5Arctan \frac{1}{239} La déduire de la formule de Gauss Je n'ai pas d'idée je me suis lancer dans des calculs de tangente mais j'arrive sur des fractions infames. _ Et je dois démontrer ...

Merci beaucoup, c'est vrai que c'est plutôt logique, et nan justement je sais utiliser ma calto et j'ai essayer avec maple pour le même résultat. j'ai une autre question en cours je suis parfois complètement larguer par des factorisation ou des développements, connaissez vous un bon moyen de s'entra...

Bonjour, j'ai deux petites questions:

1) Pourquoi peut t'ont dire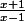 >0 équivaut à (x+1)*(x-1)>0

2) Soit f(x)= x + ln(x²-1)

Je trouve comme limite en -1 et 1 -infini
Mais sur ma calto, j'ai deux limites réelles qui apparaissent?

Merci d'avance

Oulah j'ai jamais fait additionner un élement et un ensemble, pourrais je avoir plus d'indications?

Ok, suite a ma journée de cours j'ai essayé d'exploiter ton idée, donc j'ai fait:

Z appartient a C\ a/c

j'ai posé l'équation et j'en suis arrivé à

z=

Donc si je peux conclure que z appartient a C\ -d/c c'est gagné?

C'est a dire, =Z?

Les ensembles sont C\ d/c C\ a/c

et merci pour la simplification

Bonjour j'aurais deux question a vous poser: 1) Soit f une homographie de forme \frac{az+b}{cz+d} et ad-bd diffèrent de 0, montrer que f est bijective Alors j'ai montré facilement l'injectivité mais je ne trouve pas pour la surjectivité, je prend un f dans l'ensemble d'arrivé mais je ne vois pas quo...

Ah d'accord, c'est un angle remarquable je suis censé en apprendre d'autres?

Merci beaucoup.

Ok merci beaucoup, mais j'ai pas vu cette formule en cours donc comment pourrais je faire autrement?

Bonjour, j'ai un problème sur un exo: Trouver le module et argument de a) 1+i(1+ \sqrt2 ) j'ai le module \sqrt(4+2sqrt2) mais pas l'argument b) \sqrt(10+2sqrt5) +i(1- \sqrt5 ) c) \frac {tan\phi-i}{tan\phi+i} J'ai le module du B mais je n'arrive pas a trouver les arguments et pour le ...

Bah c'était pas sorcier

Merci beaucoup.

Bah dans ce cas la, si on a f1(x)=f1(y) alors f(x)=f(y) et puisque f injective x=y et on fait de même pour f2.

Désole si je suis long ou je ne sais quoi, mais c'est le début.

Bah peut-on traduire l'énonce comme sa:

f(x),f(y) pour x,y€E1 équivaut à f1(x),f1(y)?

Oui j'avais remarqué que ce n'etait pas une composée mais je ne savais comment l'exprimer , mais faut t'il développer ou peut t-on dire que c'est evident?

Et oui, je vais m'y mettre de suite.

Peut-on dire que si f1(x)=f1(y) alors f(x)=f(y)?

Merci.