20 résultats trouvés
Revenir à la recherche avancée
- 03 Oct 2010, 18:28
- Forum: ✎✎ Lycée
- Sujet: TS question position courbe et droite
- Réponses: 5
- Vues: 761
Je sait mais jai fait tout se que je peut, soit je me retrouve avec du x^3 et je ne peut pas trouver le signe ou alors je ne voit pas ou factoriser :S
- 03 Oct 2010, 18:18
- Forum: ✎✎ Lycée
- Sujet: TS question position courbe et droite
- Réponses: 5
- Vues: 761
TS question position courbe et droite
Bonjour, je bloque sur une question, si quelqu'un pouvait m'aider, Merci
Je dois etudier la position relative d'une courbe a une droite mais je bloque
=) (1/3)(x²+x+1/x)
(1/3)(x²+x+1/x)
y=(-2/3)x -1
Voila merci de vos reponses :happy2:
Je dois etudier la position relative d'une courbe a une droite mais je bloque
y=(-2/3)x -1
Voila merci de vos reponses :happy2:
- 03 Oct 2010, 18:12
- Forum: ✎✎ Lycée
- Sujet: TS question position courbe et droite
- Réponses: 5
- Vues: 761
Je t'explique: Alors tu dois chercher pr la loi binomiale dans ce cas la, gagner au moins 10euros, et la condition pour gagner 10euros et de reussir 3 pagnier, donc cela a chercher la probabilite P(X> ou égale 3) et ensuite cela tu peut le calculer en prenant le contraire(C'est pour calculer plus ra...
- 21 Juin 2010, 08:23
- Forum: ✎✎ Lycée
- Sujet: Un petit problème de probabilité
- Réponses: 4
- Vues: 1051
Pour t'aider: On répète 9 fois, de facon independante, une épreuve a 2 issues ie "lancé un ballon vers un panier"(Loi de Bernoulli) -Succès "réussir" p=0.35 -Echec "perdre" 1-p=0.65 Soit X la variable aléatoire égale au nombre de lance de ballon vers le panier suit une loi Binomiale de paramètre 0.3...
- 20 Juin 2010, 18:16
- Forum: ✎✎ Lycée
- Sujet: Un petit problème de probabilité
- Réponses: 4
- Vues: 1051
- 27 Fév 2010, 12:40
- Forum: ✎✎ Lycée
- Sujet: Linéarisation
- Réponses: 4
- Vues: 684
La dérivée de ) c'est
c'est 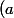cos(ax)) ,
,
et la dérivée de) c'est
c'est 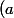-sin(ax)) ,
,
mais jvois pas trop comment cela peut m'aider? :briques:
et la dérivée de
mais jvois pas trop comment cela peut m'aider? :briques:
- 27 Fév 2010, 12:26
- Forum: ✎✎ Lycée
- Sujet: Linéarisation
- Réponses: 4
- Vues: 684
Linéarisation
Bonjour, Je dois linéariser f(x)=cos^4(x) et ensuite déterminer une primitive, je voudrais savoir si ma linéarisation et bonne, cos^4(x)=\frac{cos(4x)+4cos(2x)+3}{8} , si celle-ci est bonne je bloque sur la primitive, Si quelqu'un pourrait m'aider :briques:
- 27 Fév 2010, 12:03
- Forum: ✎✎ Lycée
- Sujet: Linéarisation
- Réponses: 4
- Vues: 684
Merci beaucoup j'ai trouver j'ai mis F(x)=P(x)e^{2x} , et P(x) est un polynôme de degré 3, comme resultat et avec la methode d'identification, j'ai trouvé F(x)=(\frac{1}{2}x^3-\frac{3}{4}x^2+\frac{3}{4}x-\frac{3}{8})e^{2x} , J'ai un peu la flemme de verifier vu l'heur...
- 26 Fév 2010, 22:25
- Forum: ✎✎ Lycée
- Sujet: Blocage sur les primitives
- Réponses: 3
- Vues: 360
Blocage sur les primitives
Bonjour,
Je n'arrive pas a trouver la primitive de=x^3e^{2x}) ,
,
Merci de votre aide :briques:
Je n'arrive pas a trouver la primitive de
Merci de votre aide :briques:
- 26 Fév 2010, 21:41
- Forum: ✎✎ Lycée
- Sujet: Blocage sur les primitives
- Réponses: 3
- Vues: 360
Merci beaucoup à toi pour ton aide précieuse, jvien de comprendre , je vais me coucher moin con se soir ^^, bonne soirée.. et bonne nuit.
- 07 Fév 2010, 21:45
- Forum: ✎✎ Lycée
- Sujet: Bloque sur un exercice d'exponentielle avec suite
- Réponses: 17
- Vues: 1560
- 07 Fév 2010, 21:41
- Forum: ✎✎ Lycée
- Sujet: Bloque sur un exercice d'exponentielle avec suite
- Réponses: 17
- Vues: 1560
Jai un doute mais jpense que f(1/n) converge vers 1 maisjme suis tromper en calculant la limite de f(x) quand celle ci tend vers 0, et la jbloque a chercher la limite car a chaque foix cela me fait une forme indetermine ^^
- 07 Fév 2010, 21:34
- Forum: ✎✎ Lycée
- Sujet: Bloque sur un exercice d'exponentielle avec suite
- Réponses: 17
- Vues: 1560
- 07 Fév 2010, 21:22
- Forum: ✎✎ Lycée
- Sujet: Bloque sur un exercice d'exponentielle avec suite
- Réponses: 17
- Vues: 1560
Pour la convergence, je vois pas pourquoi c'est marquer en deduire car d'accord
Un=(e-1)f(1/n) mais il faudrait chercher la limite en +inifini de (1/x)/(e(1/x)-1) et quel soit de 1 pour que la suite converge vers e-1 ?
Un=(e-1)f(1/n) mais il faudrait chercher la limite en +inifini de (1/x)/(e(1/x)-1) et quel soit de 1 pour que la suite converge vers e-1 ?
- 07 Fév 2010, 21:14
- Forum: ✎✎ Lycée
- Sujet: Bloque sur un exercice d'exponentielle avec suite
- Réponses: 17
- Vues: 1560
Sa y ait jai reussi, je mettais trompé dans les signes ^^, maintenant je vais matteler a la derniere question ^^, merci beaucoup pour ton aide.
- 07 Fév 2010, 21:05
- Forum: ✎✎ Lycée
- Sujet: Bloque sur un exercice d'exponentielle avec suite
- Réponses: 17
- Vues: 1560
Merci beaucoup, j'ai compris maintenant, mais il me reste un problème j'ai calculer
Un=(1/n)((1-e)/(1-e(1/n))) mais je ne trouve pas Un=(e-1)f(1/n)?
Un=(1/n)((1-e)/(1-e(1/n))) mais je ne trouve pas Un=(e-1)f(1/n)?
- 07 Fév 2010, 20:57
- Forum: ✎✎ Lycée
- Sujet: Bloque sur un exercice d'exponentielle avec suite
- Réponses: 17
- Vues: 1560
Sa Majesté a écrit:Salut
1+exp(1/n)+exp(2/n)+...+exp((n-1)/n) est la somme des termes d'une suite géométrique de raison q=exp(1/n)
Comment tu as fait pour trouver directement la raison, car c'est sa qui me bloque?
- 07 Fév 2010, 20:37
- Forum: ✎✎ Lycée
- Sujet: Bloque sur un exercice d'exponentielle avec suite
- Réponses: 17
- Vues: 1560
- 07 Fév 2010, 20:33
- Forum: ✎✎ Lycée
- Sujet: Bloque sur un exercice d'exponentielle avec suite
- Réponses: 17
- Vues: 1560
Bloque sur un exercice d'exponentielle avec suite
Sur mon DM il y a juste cet exo qui me pose problème ( si qqun pourais m'aider :we: ): On considère la fonction f définie sur ]0;+infini[ par: f(x)= x/(exp(x)-1) 1°) Déterminer la limite de la fonction f en 0. Déterminer la limite de la fonction en +infini. 2°) Soit (Un) la suite définie pour tout n...
- 07 Fév 2010, 20:17
- Forum: ✎✎ Lycée
- Sujet: Bloque sur un exercice d'exponentielle avec suite
- Réponses: 17
- Vues: 1560
- 20 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
