61 résultats trouvés
Revenir à la recherche avancée
Recherche du volume
Bonsoir tout le monde, je remercie d'avance tous ceux qui prendront le temps de m'aider! Voici un exercice de chimie sur lequel je bloque : Quels volumes V1 et V2 en mL de solution d'acide chlorhydrique aux concentrations apportée C1=0,250 mol.L-1 et C2=0,750 mol.L-1 faut-il mélanger pour obtenir 50...
- 14 Sep 2013, 20:05
- Forum: ☣ Chimie
- Sujet: Recherche du volume
- Réponses: 2
- Vues: 437
- 04 Jan 2013, 17:29
- Forum: ✎✎ Lycée
- Sujet: Equation et inéquation avec logarithme népérien
- Réponses: 9
- Vues: 684
Ah pardon, je n'avais pas réalisé que c'était une inéquation ! Donc on résout d'abord X^2-3X-4 \geq 0 S_X=]-\infty;-1] \cup [4;+\infty[ Ensuite S_x=]0;e^{-1}]\cup[e^4;+\infty[ Isn't it ? Ah d'accord, je comprend! Merci beaucoup! Je voulais poser une autre question qui n'a pas de rapport avec cet ex...
- 04 Jan 2013, 17:16
- Forum: ✎✎ Lycée
- Sujet: Equation et inéquation avec logarithme népérien
- Réponses: 9
- Vues: 684
Eh bien, lorsqu'il s'agit d'une inéquation, la solution est une intervalle non? L'expression doit être supérieure ou égale à 0, donc d'un côté je met 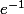 car c'est la plus "petite" des deux racines et de l'autre +oo. Enfin... je pense :marteau:
car c'est la plus "petite" des deux racines et de l'autre +oo. Enfin... je pense :marteau:
- 04 Jan 2013, 16:49
- Forum: ✎✎ Lycée
- Sujet: Equation et inéquation avec logarithme népérien
- Réponses: 9
- Vues: 684
Carpate a écrit:Pour le 2), je ne vois pas d'où tu sors ce S = []
Quelles sont les racines de?
Ah oui, je me suis trompé. En calculant delta etc, je trouve finalement que x=-1 ou x=4
Donc S= [
- 04 Jan 2013, 16:39
- Forum: ✎✎ Lycée
- Sujet: Equation et inéquation avec logarithme népérien
- Réponses: 9
- Vues: 684
Equation et inéquation avec logarithme népérien
Bonjour à tous, je vous remercie d'avance pour votre aide! J'ai fait un exercice, mais je ne suis pas sure d'avoir tout fait correctement voici l'énoncé : 1) Résoudre l'équation X^2 - X - 6 = 0 . En déduire les solutions de l'équation (ln x)^2 - ln x - 6 = 0 . J'ai tout d'abord cherché les r...
- 04 Jan 2013, 16:22
- Forum: ✎✎ Lycée
- Sujet: Equation et inéquation avec logarithme népérien
- Réponses: 9
- Vues: 684
- 21 Oct 2012, 11:52
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
Si on enlève les carrés ça donne
Donc
Donc on revient au meme! Ca fait 0 = 4, je comprend pas comment faire pour trouver l = ...
- 21 Oct 2012, 11:44
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
raito123 a écrit:Tu t'es trompé dans le passage de la 3éme à la 4éme ligne.
L'expression de Un est fausse. c'est
Ben pour "passer 0,5 de l'autre coté", il faut diviser -8 par 0,5 non? Ou c'est pas du tout ça qu'il faut faire?
- 21 Oct 2012, 11:38
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
Euh... ah mince, je me suis trompé à la dernière ligne. l+4 =l mais après on trouve 4 = l-l donc.. en fait je vois pas où j'ai pu me tromper... Donc d'après les deux dernières lignes on a \frac{-16}{2^n}=-8^n ????? Non en effet. Mais on ne peut pas plus simplifier donc u_n =sqrt {16 - \frac{-16}{2^n...
- 21 Oct 2012, 11:21
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
Je viens de faire les deux questions suivantes et j'aimerai savoir si j'ai bien répondu : 4) On se propose d'obtenir l'expression de u_n en fonction de n. a) v est le suite définie sur lN par v_n = u_{n}^2 - 16 . Démontrer que v est géométrique. b) En deduire l'expression de v_n puis de u_n en fonct...
- 21 Oct 2012, 10:59
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
Est ce que pour toi les deux premières lignes sont equivalentes ?? Ce n'est pas plus facile de faire : l = sqrt{0,5l^2+8} sqrt{0,5l^2+8}^2 = l^2 0,5l^2+8 = l^2 ? Bon, j'ai fait : l^2 = 0,5l^2+8 0,5l^2+8-l^2 = 0 0,5l^2-l = -8 l^2-l^2 = -16 l^2 = sqrt{l^2-16} l = l-4 l+4 = l 4 = 2l donc l = 2
- 21 Oct 2012, 10:28
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
Bon, finalement voici ce que j'ai fait :
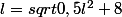
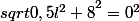
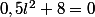
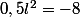
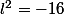
Mais si j'enleve le carré, j'obtiens -4, ce qui n'est pas le bon résultat!! Comment faire?? :mur:
Mais si j'enleve le carré, j'obtiens -4, ce qui n'est pas le bon résultat!! Comment faire?? :mur:
- 21 Oct 2012, 09:27
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
Ben lorsque je résoud cette équation, je trouve toujours un nombre négatif... je comprend pas pourquoi.
Ou alors peut-on juste dire que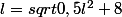 ??
??
Ou alors peut-on juste dire que
- 21 Oct 2012, 01:48
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
raito123 a écrit:heu non ce n'est pas cela. tu as l'expression u(n+1)^2 = 0.5u(n)^2+8, comment tu fais ensuite ?
Ben...
On en déduit par unicité de la limite d'une suite au
- 21 Oct 2012, 01:41
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
raito123 a écrit:Pourquoi la limite de u(n+1)^2 est l ? ce n'est pas l^2 ? et tu ne trouve pas bizarre le fait que l soit négatif. Toi-même t'as affirmé que 0<l<8 non ?
Oui c'est vrai... je suis un peu perdue, l'équation à résoudre est donc
- 21 Oct 2012, 01:29
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
Ah d'accord, je comprend. Voici les deux questions suivantes auxquelles j'ai répondu (je voudrais savoir si c'est juste) : 3)a) Justifier que la suite u est convergente. J'ai dit que : d'après la question précédente, la suite u est croissante et majorée par 8 donc elle converge vers un nombre réel l...
- 21 Oct 2012, 01:17
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
raito123 a écrit:Oui vu que racine(40)<racine(49)=7<8 ( par contre y a une petite erreur u(n+1)<64 et non pas 8 )
Mais d'où sort le racine de 49 (ou 7) ? (en effet, j'ai fait une faute de frappe)
- 21 Oct 2012, 00:42
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
Pour lhérédité, il faut supposer que 0 \leq u_n \leq u_{n+1} \leq 8 et en déduire que 0 \leq u_{n+1} \leq u_{n+2} \leq 8 ... Voici ce que j'ai fait pour l'hérédité : 0 \leq u_{n} \leq u_{n+1} \leq 8 donc 0 \leq u_{n}^2 \leq u_{n+1}^2 \leq 8 donc 0 \leq 0,5u_{n}^2 \leq 0,5u_{n+1}^2 \leq 32 donc 8 \...
- 21 Oct 2012, 00:32
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
Merci beaucoup! u_0 = 0, j'avais oublié de le préciser... Finalement j'ai trouvé que u_1 = sqrt {8} et u_2 = environ 3,068 ! Par contre, dans la question suivante ils me demandent de démontrer par récurrence que 0 \leq u_n \leq u_{n+1} \leq 8 ... A l'initialisation je trouve 0 \leq u_0 \leq u_{1} \l...
- 21 Oct 2012, 00:09
- Forum: ✎✎ Lycée
- Sujet: Récurrence avec une racine carrée (DM de TS)
- Réponses: 28
- Vues: 2284
- 61 résultats trouvés - Page 1 sur 4 • 1, 2, 3, 4
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
