Equation et inéquation avec logarithme népérien
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Silver-DN!
- Membre Naturel
- Messages: 61
- Enregistré le: 27 Sep 2009, 15:09
-
 par Silver-DN! » 04 Jan 2013, 15:22
par Silver-DN! » 04 Jan 2013, 15:22
Bonjour à tous, je vous remercie d'avance pour votre aide! J'ai fait un exercice, mais je ne suis pas sure d'avoir tout fait correctement voici l'énoncé :
1) Résoudre l'équation
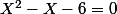
. En déduire les solutions de l'équation
^2 - ln x - 6 = 0)
.
J'ai tout d'abord cherché les racines à l'aide de delta et je trouve donc que x=-2 et x=3, donc j'en déduit que S={
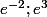
} car
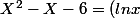^2 - ln x - 6)
2) Résoudre l'équation
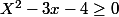
. En déduire les solutions de l'inéquation
^2 - 3ln x - 4 \geq 0)
Donc ici j'ai utilisé la même méthode et je trouve finalement que S = [
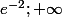
]
Je ne suis pas sure du tout de mes réponses (et j'ai du mal a expliquer ma démarche...)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Jan 2013, 15:25
par Carpate » 04 Jan 2013, 15:25
Silver-DN! a écrit:Bonjour à tous, je vous remercie d'avance pour votre aide! J'ai fait un exercice, mais je ne suis pas sure d'avoir tout fait correctement voici l'énoncé :
1) Résoudre l'équation
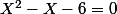
. En déduire les solutions de l'équation
^2 - ln x - 6 = 0)
.
J'ai tout d'abord cherché les racines à l'aide de delta et je trouve donc que x=-2 et x=3, donc j'en déduit que S={
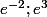
} car
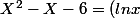^2 - ln x - 6)
2) Résoudre l'équation
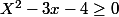
. En déduire les solutions de l'inéquation
^2 - 3ln x - 4 \geq 0)
Donc ici j'ai utilisé la même méthode et je trouve finalement que S = [
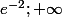
]
Je ne suis pas sure du tout de mes réponses (et j'ai du mal a expliquer ma démarche...)
Ca ne t'interpelle pas d'écrire lnx = -2 ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Jan 2013, 15:32
par Carpate » 04 Jan 2013, 15:32
Silver-DN! a écrit:Bonjour à tous, je vous remercie d'avance pour votre aide! J'ai fait un exercice, mais je ne suis pas sure d'avoir tout fait correctement voici l'énoncé :
1) Résoudre l'équation
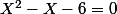
. En déduire les solutions de l'équation
^2 - ln x - 6 = 0)
.
J'ai tout d'abord cherché les racines à l'aide de delta et je trouve donc que x=-2 et x=3, donc j'en déduit que S={
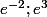
} car
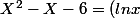^2 - ln x - 6) Tu peux écrire : on résous
Tu peux écrire : on résous ^2 - ln x - 6 = 0) en posant X = lnx(avec x >0), on se ramène à l'équation
en posant X = lnx(avec x >0), on se ramène à l'équation 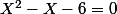 dont les racines sont -2 et 3 d'où
dont les racines sont -2 et 3 d'où 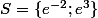
2) Résoudre l'équation
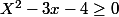
. En déduire les solutions de l'inéquation
^2 - 3ln x - 4 \geq 0)
Donc ici j'ai utilisé la même méthode et je trouve finalement que S = [
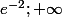
]
Je ne suis pas sure du tout de mes réponses (et j'ai du mal a expliquer ma démarche...)
Pour le 2), je ne vois pas d'où tu sors ce S = [
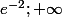
]
Quelles sont les racines de
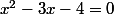
?
-
Silver-DN!
- Membre Naturel
- Messages: 61
- Enregistré le: 27 Sep 2009, 15:09
-
 par Silver-DN! » 04 Jan 2013, 15:39
par Silver-DN! » 04 Jan 2013, 15:39
Carpate a écrit:Pour le 2), je ne vois pas d'où tu sors ce S = [
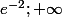
]
Quelles sont les racines de
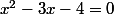
?
Ah oui, je me suis trompé. En calculant delta etc, je trouve finalement que x=-1 ou x=4
Donc S= [
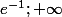
[ ???
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Jan 2013, 15:42
par Carpate » 04 Jan 2013, 15:42
Silver-DN! a écrit:Ah oui, je me suis trompé. En calculant delta etc, je trouve finalement que x=-1 ou x=4
Donc S= [
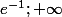
[ ???
C'est bien X =-1 et 4
Je ne vois toujours pas ce que vient faire ce

-
Silver-DN!
- Membre Naturel
- Messages: 61
- Enregistré le: 27 Sep 2009, 15:09
-
 par Silver-DN! » 04 Jan 2013, 15:49
par Silver-DN! » 04 Jan 2013, 15:49
Eh bien, lorsqu'il s'agit d'une inéquation, la solution est une intervalle non? L'expression doit être supérieure ou égale à 0, donc d'un côté je met
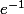
car c'est la plus "petite" des deux racines et de l'autre +oo. Enfin... je pense :marteau:
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Jan 2013, 16:01
par Carpate » 04 Jan 2013, 16:01
Silver-DN! a écrit:Eh bien, lorsqu'il s'agit d'une inéquation, la solution est une intervalle non? L'expression doit être supérieure ou égale à 0, donc d'un côté je met
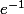
car c'est la plus "petite" des deux racines et de l'autre +oo. Enfin... je pense :marteau:
Ah pardon, je n'avais pas réalisé que c'était une inéquation !
Donc on résout d'abord
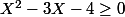
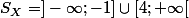
Ensuite
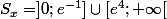
Isn't it ?
-
Silver-DN!
- Membre Naturel
- Messages: 61
- Enregistré le: 27 Sep 2009, 15:09
-
 par Silver-DN! » 04 Jan 2013, 16:16
par Silver-DN! » 04 Jan 2013, 16:16
Carpate a écrit:Ah pardon, je n'avais pas réalisé que c'était une inéquation !
Donc on résout d'abord
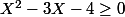
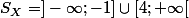
Ensuite
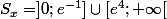
Isn't it ?
Ah d'accord, je comprend! Merci beaucoup! Je voulais poser une autre question qui n'a pas de rapport avec cet exercice mais sur laquelle je bloque depuis un bon moment : le but est d'exprimer en fonction de ln2 et ln3 l'expression
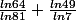
A la fin je trouve
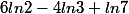
et je n'arrive pas a me débarrasser du ln7 ! Est-ce qu'il y a une solution ou il faut juste laisser comme ça?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Jan 2013, 16:25
par Carpate » 04 Jan 2013, 16:25
Silver-DN! a écrit:Ah d'accord, je comprend! Merci beaucoup! Je voulais poser une autre question qui n'a pas de rapport avec cet exercice mais sur laquelle je bloque depuis un bon moment : le but est d'exprimer en fonction de ln2 et ln3 l'expression
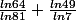
A la fin je trouve
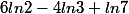
et je n'arrive pas a me débarrasser du ln7 ! Est-ce qu'il y a une solution ou il faut juste laisser comme ça?
}{ln(3^4)}+\frac{ln(7^2)}{ln7} = \frac32 \quad \frac{ln2}{ln3} +2)
-
Silver-DN!
- Membre Naturel
- Messages: 61
- Enregistré le: 27 Sep 2009, 15:09
-
 par Silver-DN! » 04 Jan 2013, 16:29
par Silver-DN! » 04 Jan 2013, 16:29
Carpate a écrit:}{ln(3^4)}+\frac{ln(7^2)}{ln7} = \frac32 \quad \frac{ln2}{ln3} +2)
Ah, mais c'était super simple en fait!! Merci beaucoup Carpate

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
