104 résultats trouvés
Revenir à la recherche avancée
- 01 Fév 2015, 19:15
- Forum: ✯✎ Supérieur
- Sujet: Espaces homéomorphes ou non
- Réponses: 10
- Vues: 892
J'ai trouvé (sur un forum) la réponse à ma question. Soit  un homéomorphisme, il induit donc un homéomorphisme de
un homéomorphisme, il induit donc un homéomorphisme de \}) sur
sur ) . Or le premier espace est simplement connexe et pas le second, ce qui est contradictoire.
. Or le premier espace est simplement connexe et pas le second, ce qui est contradictoire.
- 01 Fév 2015, 19:06
- Forum: ✯✎ Supérieur
- Sujet: Espaces homéomorphes ou non
- Réponses: 10
- Vues: 892
à jlb, soit 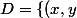\in S\;|\;y=0\}) , et
, et  un homéomorphisme, si on enlève
un homéomorphisme, si on enlève ) à
à  , l'ensemble obtenu peut-être connexe et même simplement connexe : l'image de D peut être une demi-droite du plan.
, l'ensemble obtenu peut-être connexe et même simplement connexe : l'image de D peut être une demi-droite du plan.
- 01 Fév 2015, 18:17
- Forum: ✯✎ Supérieur
- Sujet: Espaces homéomorphes ou non
- Réponses: 10
- Vues: 892
Espaces homéomorphes ou non
Bonjour, voici mon problème : On munit S=\{(x,y)\in\mathbb{R}^2\;|\;0\leq y\} de la topologie induite. Ma question est S et \mathbb{R}^2 sont-ils homéomorphes ? Je pense que non mais je n'ai pas trouvé une preuve complète et rigoureuse. Si quelqu'un connait un argument simple je lui en serai...
- 01 Fév 2015, 14:45
- Forum: ✯✎ Supérieur
- Sujet: Espaces homéomorphes ou non
- Réponses: 10
- Vues: 892
Bonjour,
pour égayer tes révisions tu pourras aller voir là : http://www.apprendre-en-ligne.net/MADIMU2/INDEX.HTM
Bon courage.
pour égayer tes révisions tu pourras aller voir là : http://www.apprendre-en-ligne.net/MADIMU2/INDEX.HTM
Bon courage.
- 17 Aoû 2010, 09:43
- Forum: ✎✎ Lycée
- Sujet: que réviser avant rentrer terminal spé math ?
- Réponses: 9
- Vues: 2933
Je reviens, et tire encore sur la corde. L'implication serait-elle vraie si 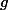 était continue et ouverte ?
était continue et ouverte ?
Merci d'avance pour les réponses.
Merci d'avance pour les réponses.
- 14 Aoû 2010, 15:09
- Forum: ✯✎ Supérieur
- Sujet: composée par une application ouverte
- Réponses: 6
- Vues: 1059
J'en ai une : 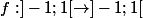 telle que
telle que
[CENTER]=\frac{x-1}{2}$) si
si 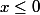 et
et =\frac{x+1}{2}$) si
si 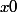 [/CENTER]
[/CENTER]
Si je ne me trompe pas=\frac{x-1}{2}$) pour tout
pour tout 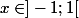 .
.
Encore merci Finrod.
[CENTER]
Si je ne me trompe pas
Encore merci Finrod.
- 14 Aoû 2010, 13:55
- Forum: ✯✎ Supérieur
- Sujet: composée par une application ouverte
- Réponses: 6
- Vues: 1059
ça marche aussi pour moi 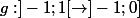 est ouverte et discontinue en 0. Par contre, il me faudrait
est ouverte et discontinue en 0. Par contre, il me faudrait 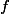 discontinue et telle que
discontinue et telle que 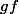 est continue.
est continue.
- 14 Aoû 2010, 13:43
- Forum: ✯✎ Supérieur
- Sujet: composée par une application ouverte
- Réponses: 6
- Vues: 1059
Merci Finrod pour cette réponse rapide. Pour la fonction $g$ donnée je trouve que l'image directe de $]-\frac{1}{2};\frac{1}{2}[$ est $]-1;0]-\{-\frac{1}{2}\}$ donc si je ne me suis pas trompé cette fonction n'est pas ouverte. Même en réduisant le saut on retrouve un intervalle plus petit dont l'ima...
- 14 Aoû 2010, 12:43
- Forum: ✯✎ Supérieur
- Sujet: composée par une application ouverte
- Réponses: 6
- Vues: 1059
composée par une application ouverte
Bonjour, en relisant des cours, je me suis demandé si l'implication suivante était vraie : soit $f:E\rightarrow F$ une application, et $g:F\rightarrow G$ une application ouverte (E,F,G sont des espaces topologiques) a t-on ( $gof$ continue) $\Rightarrow$ ( $f$ continue) ? Si vous aviez un contre-exe...
- 14 Aoû 2010, 11:46
- Forum: ✯✎ Supérieur
- Sujet: composée par une application ouverte
- Réponses: 6
- Vues: 1059
Bonsoir,
peut être as tu vu ce document : http://www.emis.de/journals/JIPAM/images/043_00_JIPAM/043_00.pdf
peut être as tu vu ce document : http://www.emis.de/journals/JIPAM/images/043_00_JIPAM/043_00.pdf
- 13 Aoû 2010, 22:21
- Forum: ✯✎ Supérieur
- Sujet: coefficients binomiaux
- Réponses: 3
- Vues: 1138
Bonjour,
Dans le premier membre de ton égalité, on peut faire apparaître le coefficient d'un terme en sin(x) or ce terme peut prendre plusieur valeurs si son coefficient est non nul.
Dans le premier membre de ton égalité, on peut faire apparaître le coefficient d'un terme en sin(x) or ce terme peut prendre plusieur valeurs si son coefficient est non nul.
- 04 Aoû 2010, 15:12
- Forum: ✎✎ Lycée
- Sujet: Determiner a et b tels que ...
- Réponses: 2
- Vues: 761
Décidément je ne trouve jamais les réponses les plus simples.
Pour la deuxième question, même si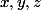 ne peuvent être nuls (par exemple si
ne peuvent être nuls (par exemple si 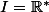 ) on peut déduire de la relation
) on peut déduire de la relation =f(x)+f(y)+f(z)$) que
que 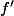 est constante.
est constante.
Pour la deuxième question, même si
- 04 Aoû 2010, 13:09
- Forum: ✯✎ Supérieur
- Sujet: Logarithme népérien
- Réponses: 7
- Vues: 1060
Bonjour, Si on suppose $f$ définie et dérivable sur $\mathbb{R}_{+}$ et telle que $f(xy)=f(x)+f(y)$ pour tous $x,y\in\mathbb{R}_{+}$ alors la fonction $g$ définie comme précédemment mais sur $\mathbb{R}_{+}$ vérifie : $g'(y)=xf'(xy)$ pour tout $y\in\ma...
- 04 Aoû 2010, 11:58
- Forum: ✯✎ Supérieur
- Sujet: Logarithme népérien
- Réponses: 7
- Vues: 1060
- 03 Aoû 2010, 14:08
- Forum: ✎✎ Lycée
- Sujet: Calcul de limite, niveau Terminale S
- Réponses: 3
- Vues: 1248
J'ai trouvé mon erreure, je ne tiens compte que du nombre de personnes pour chaque mois alors qu'il faudrait distinguer lesquelles. Et ce que je croyait être une erreur n'en est donc pas une.
- 02 Aoû 2010, 16:21
- Forum: ✯✎ Supérieur
- Sujet: Probabilité et analyse combinatoire
- Réponses: 4
- Vues: 1247
Oui, le tout c'est que le correcteur ne pense pas que tu crois le logarithme défini pour $x\leq 0$ . La racine cubique d'un négatif existe bien, par exemple $\sqrt[3]{-8}=-2$ , c'est l'unique réel $y$ qui vérifie $y^3=-8$ . Pour $x\mapsto x^{\frac{6}{5}}$ le domaine est toujours $\mathbb{R}$ . Je pr...
- 02 Aoû 2010, 14:14
- Forum: ✯✎ Supérieur
- Sujet: Puissance fractionnaire
- Réponses: 9
- Vues: 1438
Pour répondre aux exemples je dirai (ce qui ne suit pas le cours dont je parle plus haut) : 1) $x\mapsto x^{\frac{4}{3}}$ le domaine est $\mathbb{R}$ tant qu'on ne se place pas dans une famille de fonctions puissance, pourquoi se restreindre ? 1') $x\mapsto x^{\frac{5}{3}}$ le domaine est encore $\m...
- 02 Aoû 2010, 13:19
- Forum: ✯✎ Supérieur
- Sujet: Puissance fractionnaire
- Réponses: 9
- Vues: 1438
ça y est, j'ai compris. En fait c'est plutôt une question de convention. Je viens de trouver un cours qui distingue les expressions $\sqrt[3]{x}$ et $x^{\frac{1}{3}}$ , la première étant définie sur $\mathbb{R}$ et l'autre sur $\mathbb{R}_{+}^{*}$ . La deuxième expression renvoie à la définition fai...
- 02 Aoû 2010, 12:44
- Forum: ✯✎ Supérieur
- Sujet: Puissance fractionnaire
- Réponses: 9
- Vues: 1438
A mon tour de demander où est l'erreur. Je procède autrement : l'ensemble de toutes les possibilités (l'univers) est un ensemble de combinaisons avec répétition, à chaque mois j'associe le nombre compris entre 0 et 20 de personnes nées ce mois là, la somme totale doit être égale à 20. Il y en a $\Ga...
- 02 Aoû 2010, 10:28
- Forum: ✯✎ Supérieur
- Sujet: Probabilité et analyse combinatoire
- Réponses: 4
- Vues: 1247
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
