Forum de Mathématiques: Maths-Forum

Bon j'ai bien compris qu'il n'y avait pas de solution analytique... J'ai donc décidé de chercher une solution approchée en raisonnant ainsi : Pour des soucis d'homogénéité, on doit trouver r = \alpha R avec 0 < \alpha < 1 Comme on a l'expression de l'aire grise, il suffit de remplacer r par \alpha R...

Donc grosso modo, 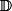ne sert à rien, car il ne peut pas être utilisé en arithmétique comme ses collègues et 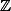et il n'a pas la structure suffisante pour être intéressant comme , et ...

Merci à vous deux ^^

Bonjour Au collège, on nous apprend les ensembles de nombres de \mathbb N à \mathbb R , en passant par \mathbb D , les nombres décimaux. Pourtant, par la suite, on abandonne cette ensemble. Même dans la théorie des groupes, des anneaux, des corps... on ne s'intéresse jamais à \mathbb D en prépa. Alo...

Pourtant je vois dans le programme de maths de MP-MP* (disponible sur http://www.prepas.org): « Série exponentielle : étant donné une algèbre normée A de dimension finie ayant e pour élément unité alors, pour tout élément u de A, la série \sum \frac{u^n}{n!} est absolument convergente ; par définit...

en les calculant peut etre .. Nan, les interversions de limites ne se justifient pas aussi simplement... Soit a un point de A, ou une borne de A. Si (f_n) converge uniformément vers f sur A, et si pour tout n \in \mathbb N , f_n admet une limite b_n en a, Alors f admet une limite en a, et o...

Bonsoir Dominique.
J'en prends note, je tâcherai d'y faire attention.

Vraiment du hors programme ou c'était parce que tu n'avais pas tout revu :marteau: ?? Nan nan, vraiment du hors programme, mon prof de physique a dit que tous ceux qui avaient eu plus de 3 étaient des génies XD Bon il exagérait, mais franchement y avait énormément de hors programme dans cette épreu...

Oui, d'ailleurs, si vous avez lu mon post, vous avez pu constater que je n'étais pas très organisé en SUP... donc là je trie tous mes cours dans l'optique de la réviser cette année ^^ A l'écrit de CCP, toute l'optique est l'optique de sup... Tu parles de CCP de cette année ? c'était même du hors pro...

tu as raison : certains résultats ne sont pas acceptés à certains niveaux, mais tout à fait habituels à d'autre. Exemple, j'imagine qu'en première, on n'admet pas qu'un étudiant balance les solutions d'une équation de degré 2 sans preuve... alors qu'en Master 2, cela ne pose pas de problème évidemm...

Et puis un DL n'est pas un polynôme infini (au passage, polynome infini = série entière), parce qu'un DL possède un ordre, qui est un majorant (souvent égal) au degré de la partie polynomial du DL (sans parler du reste du DL) Oui, je confond un peu les deux -_-" merci de la précision =D d'une,...

Ben si, c'est exactement pareil : e^x = 1 + x + x²/2 + ... e^(ix) = 1 + x + (ix)²/2 + ... les moins que tu remarques proviennent des puissances du coefficient complexe i dans (ix) Oui, je m'en suis rendu compte après :$ Mais je suppose que le démontrer à partir de l'exponentiel est faux ? à cause d...

Quand tu étudies le numérateur de ta dérivée, le -x²+2x-b-3, tu trouves




Donc tu dois juste trouver les valeurs de b pour que ta dérivée ne s'annule pas en changeant de signe, et ainsi ta fonction n'aura pas d'extremum local.

Mais >< Nan, un équivalent est le premier, voire les deux premiers termes d'un DL. Un DL est un polynôme infini. Il s'obtient à partir de la formule de Taylor-Young appliqué à la fonction en un point. Si f et g possèdent deux D.L.n, alors f + g possède un D.L.n qui s'obtient en effectuant la somme d...

Et si u est négatif hein ?!

Nan, y a autre chose...

Ca m'arrive aussi de confondre sin et cos XD

Bon je cherche une explication de lycée, mais j'avoue avoir du mal...
Un bon coup d'équivalent et on en parlerait plus !

Je continue de chercher...

lim x->0 (cos(x)-1) / (x) = -1 Erreur : \frac{cos(x)-1}{x} = \frac{cos(x) - cos(0)}{x-0} En passant à la limite, on retrouve la dérivée de cos en 0 soit -sin(0) = 0 Mais de tout façon tu n'y arriveras pas comme ça, puisque tu vas obtenir une indétermination de type "0/0...

XD bon "discriminant" alors... abus de langage quand tu nous tiens...

attention a la somme de DL .. Je peux additionner des DL comme je veux, ce sont les équivalents que je n'ai pas droit de sommer sans justifications, à cause des termes qui pourraient éventuellement s'annuler... Le problème des DL, c'est quand on les compose, mais là je ne vois pas où je fais une te...

Tu ne sais rien sur les exponentielles complexes, tu dois tout redémontrer ^^ e^{ix} = cos(x) + isin(x) Donc je suppose qu'en ayant un développement limité de cos(x) et sin(x) en zéro, on doit bien pouvoir retrouver que e^{ix} = 1 + ix - \frac{x^2}{2!} - i\frac{x^3}{3!} + ... +(-...

\frac{-x^2 + 2x -b -3}{(x - 1)^2} Voilà la dérivée que tu obtiens. Il va falloir étudier son signe, donc tu laisses tomber le dénominateur, il s'agit d'un carré, il est positif et n'intervient pas dans l'étude du signe. Tu t'occupes du signe du numérateur. Pour ça, tu fais l'études de cette...