Forum de Mathématiques: Maths-Forum

Merci beaucoup pour ta réponse catamat et mes excuses pour ma confusion d'hier. Je pense y arriver tout seul maintenant.

Désolé les amis, je me suis encore planté!

L'énoncé complet est: -Résoudre les inéquations suivantes:

a) ln(x²)<ln(6)
b)exp(3x)-exp(4x)=>0

Voila tout est en ordre maintenant

Bonjour vam et catamat, Je vous ai posté un message hier mais celui-ci s'est perdu... J'avais posé la condition x²>0 mais aussi x>0 avec laquelle vous n'êtes pas d'accord, je vais vous expliquer pourquoi: l'inéquation initiale est: ln(x²)<ln(x) Regardons le premier membre: l'inéquation est définie s...

Bonjour vam et merci pour ta réponse, Je reprends: ln(x²)<ln(6) il faut x²>0 et x>0 or x² est toujours >=0 donc x doit être différent de 0 il faut x>0 condition résultante: x>=0 il vient: 2*ln(x)<ln(6) <=>(2*ln(x))/2<(ln(6))/2 <=> ln(x)<1/2*ln(6) <=> ln(x)<ln(V6) cette dernière condition peut être r...

Bonjour à tous,

Je suis bloqué par cette inéquation: ln(x²)<ln(6)

Après calculs j'arrive à: ln(x)<ln(V6), est-ce que c'est correct jusque là?

Merci de me répondre Cordialement lefouineur

Merci beaucoup Pisigma,

Cela me semble correct, je vais me coucher, bonne nuit

Cordialement lefouineur

Merci pour ta réponse,

Si l'on remplace au dénominateur, on s'éloigne de la forme attendue, relis les deux premiers messages

Cordialement lefouineur

Merci Pisigma pour ta réponse rapide, Je suis arrivé à l'expression suivante: \frac{a^2*sin(B)*sin(C)*sin(B+C)}{2*sin(B+C)} ce qui conduit à: \frac{a^2*sin(B)*sin(C)*sin(A)}{2*sin(B+C)} et j'ai un sin(A) de trop!! Que faire? Cordialemen...

Bonjour à tous, J'essaye depuis plusieurs heures de démontrer cette formule pour un triangle quelconque: Aire= \frac {a^2*sin(ABC)*sin(ACB)}{2*sin(ABC+ACB)} J'ai réussi à démontrer la formule de Héron utilisant le demi périmètre du triangle puis une autre plus générale si l'o...

Bonjour Pisigma et merci pour ta réponse rapide,

Je suis arrivé à la fin du calcul.

Je te remercie aussi pour la patience dont tu as fait preuve à mon égard tout au long de ce post.

Cordialement lefouineur

Bonjour Pisigma et merci pour ta réponse,

J'ai corrigé les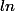 avec les valeurs absolues.

Comment revenir en u puis en x?

Cordialement lefouineur

Justement, d'oû vient le 2 au numérateur?

Cordialement lefouineur

Merci Pisigma pour ta réponse rapide, la réponse pour la première intégrale est donc: \int\frac{1}{2t-1}dt =\frac{1}{2}\int\frac{2}{2t-1}dt=\frac{1}{2}ln|2t-1| et pour la seconde: \int\frac{1}{t^2-1}dt=\frac{1}{2}ln\frac{|t-1|}{|t+1|}=ln(\frac{|t-1|}{|t+1|})^\frac{1}{2}=ln\sqrt{{\frac{|t-1|}...

Bonjour Pisigma et merci pour ta réponse, Ce que j'entends par taille normale est lisible et non rikiki comme le sont les intégrales que je poste sur le forum! J'ai essayé de m'attaquer à la seconde intégrale mais ce que j'obtiens n'est pas convaincant: \int\frac{1}{x\sqrt{x^4-x^2+1}}dx=\int\frac{du...

Bonjour Pisigma et merci pour ta réponse rapide Je reprends: \sqrt{u^2-u+1}=\frac{t^2-t+1}{2t-1} du=\frac{2(t^2-t+1)}{(2t-1)^2} donc \frac{1}{2}\int\frac{du}{\sqrt{u^2-u+1}}=\frac{1}{2}\int\frac{\frac{2(t^2-t+1)}{(2t-1)^2}}{\frac{t^2-t+1}{2t-1}}dt finalement il reste:...

Pisigma,

Je te poste ce que j'ai fait, je ne sais pas comment on poste des photos.



Cordialement lefouineur

Bonjour Pisigma et merci pour ta réponse, J'aimerai bien te poster mes calculs mais il sont trop lourds pour être écrits en latex (écriture que je ne maîtrise pas). J'ai réécrit l'intégrale en u en intégrale en t donc en remplaçant u et du par leur valeur. Mais je ne vois aucune simplification appar...

Merci pour ta correction, Pisigma. J'ai fait le calcul de u: -u+1=t²-2ut -u+2ut=t²-1 u(-1+2t)=t²-1 d'oû u=\frac{t^2-1}{2t-1} et du=\frac{2(t^2-t+1)}{(2t-1)^2}dt ce qui donne dans l'intégrale en u: \frac{1}{2}\int\frac{2\left|2t-1|\right}{(2t-1)^2}dt (après simplifications) Qu...

Bonjour Pisigma et merci pour ta réponse rapide,

Je ne comprends pas bien la coquille dans l'intégrale, c'est bien:

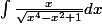dont il s'agit? pourrais-tu me détailler le calcul(changement de variable (x^2=u))

Cordialement lefouineur

Bonjour Pisigma et merci pour ta réponse rapide, J'ai corrigé l'intégrale, il vient: \int\frac{2u}{\sqrt{u^2-u+1}}du et \sqrt{u^2-u+1}=-u+t on élève au carré u^2-u+1=(t-u)^2 u^2-u+1=t^2-2ut+u^2 on simplifie -u+1=t^2-2ut -u=t^2-2ut-1 u=-t^2+2ut +1 d'oû du=(-2t+2u)dt Est-ce-que c'est b...